Упражнение 747 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник

а) \(4x^2+7x+3=0\)

\(a = 4\),  \(b = 7\),  \(c = 3\)

\( D=b^2 - 4ac=7^2-4\cdot 4\cdot 3=\)

\(=49-48=1 \),    \(\sqrt D = 1\).

\(x_{1,2} = \frac{-b\pm \sqrt D}{2a}\)

\( x_1=\frac{-7+1}{2\cdot4}=-\frac{6}{8}=-\frac{3}{4}\)

\(x_2=\frac{-7-1}{2\cdot4}=-\frac{8}{8}=-1 \)

Ответ: \(-\frac{3}{4}\);  \(-1\).

б) \(x^2+x-56=0\)

\(a = 1\),  \(b = 1\),  \(c = -56\)

\( D=b^2-4ac=1^2-4\cdot 1\cdot (-56)=\)

\(=1+224=225 \),    \(\sqrt D = 15\).

\(x_{1,2} = \frac{-b\pm \sqrt D}{2a}\)

\( x_1=\frac{-1 + 15}{2\cdot1} =\frac{14}{2}=7\).

\( x_2=\frac{-1 - 15}{2\cdot1} =-\frac{16}{2}=-8\).

Ответ: \(7\);  \(-8\).

в) \(x^2-x-56=0\)

\(a = 1\),  \(b = -1\),  \(c = -56\)

\( D=b^2 - 4ac=\)

\(=(-1)^2-4\cdot 1\cdot (-56)=\)

\(=1+224=225 \),    \(\sqrt D = 15\).

\(x_{1,2} = \frac{-b\pm \sqrt D}{2a}\)

\( x_1=\frac{-(-1) + 15}{2} =\frac{16}{2}=8\).

\( x_2=\frac{-(-1) - 15}{2} =\frac{-14}{2}=-7\).

Ответ: \(8\);  \(-7\).

г) \(5x^2-18x+16=0\)

\(a = 5\),  \(b = -18\),  \(c = 16\)

\( D=b^2 - 4ac=\)

\(=(-18)^2-4\cdot 5\cdot 16=\)

\(=324-320=4 \),   \(\sqrt D = 2\).

\(x_{1,2} = \frac{-b\pm \sqrt D}{2a}\)

\( x_1=\frac{-(-18) + 2}{2\cdot5} = -\frac{20}{10} = 2\).

\( x_2=\frac{-(-18) - 2}{2\cdot5} = \frac{16}{10} = 1,6\).

Ответ: \(2\);  \(1,6\).

д) \(8x^2+x-75=0\)

\(a = 8\),  \(b = 1\),  \(c = -75\)

\( D=b^2 - 4ac=1^2-4\cdot 8\cdot (-75)=\)

\(=1+2400=2401 \),   \(\sqrt D = 49\).

\(x_{1,2} = \frac{-b\pm \sqrt D}{2a}\)

\(x_1=\frac{-1+ 49}{2\cdot8}=\frac{48}{16}=3\).

\(x_2=\frac{-1- 49}{2\cdot8}=-\frac{50}{16}=-\frac{25}{8}=\)

\(=-3\frac18\).

Ответ: \(3\),   \(-3\frac18\).

е) \(3x^2-11x-14=0\)

\(a = 3\),  \(b = -11\),  \(c = -14\)

\( D=b^2-4ac=\)

\(=(-11)^2-4\cdot 3\cdot (-14)=\)

\(=121+168=289 \),    \(\sqrt D = 17\).

\(x_{1,2} = \frac{-b\pm \sqrt D}{2a}\)

\( x_1=\frac{-(-11) + 17}{6} =\frac{28}{6}=\frac{14}{3}=\)

\(=4\frac23\).

\( x_2=\frac{-(-11) + 17}{6} =-\frac{6}{6}=-1\).

Ответ: \(4\frac23\);  \(-1\).

ж) \(3x^2+11x-34=0\)

\(a = 3\),  \(b = 11\),  \(c = -34\)

\( D=b^2 - 4=11^2-4\cdot 3\cdot (-34)=\)

\(=121+408=529 \),    \(\sqrt D = 23\).

\(x_{1,2} = \frac{-b\pm \sqrt D}{2a}\)

\( x_1=\frac{-11+ 23}{6} = \frac{12}{6} = 2\)

\( x_2=\frac{-11- 23}{6}=-\frac{34}{6}=-\frac{17}{3}=\)

\(=-5\frac23 \).

з) \(x^2-x-1=0\)

\(a = 1\),  \(b = -1\),  \(c = -1\)

\( D=b^2 - 4ac=\)

\(=(-1)^2-4\cdot 1\cdot (-1)=\)

\(=1+4=5 \),    \(\sqrt D = \sqrt5\).

\(x_{1,2} = \frac{-b\pm \sqrt D}{2a}\)

\( x_1=\frac{1+ \sqrt{5}}{2} \).

\( x_2=\frac{1- \sqrt{5}}{2} \).

Ответ: \(\frac{1+ \sqrt{5}}{2} \);  \(\frac{1- \sqrt{5}}{2} \).

Пояснения:

Использованные приёмы и формулы:

Количество корней квадратного уравнения \(ax^2+bx+c=0\) зависит от дискриминанта. Формула дискриминанта:

\(D=b^2-4ac\).

– если \(D>0\), то уравнение имеет два корня:

\(x_1 =\frac{-b+\sqrt{D}}{2a}\);

\(x_2 =\frac{-b-\sqrt{D}}{2a}\).

– если \(D=0\), то уравнение имеет один корень:

\(x =-\frac{b}{2a}\).

– если \(D<0\), то уравнение не имеет корней.

\(m > p\), \(n > m\), \(n < q\)

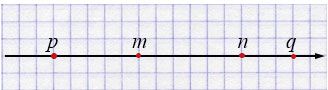
\(p < n\),  \(p < q\),  \(q > m.\)

Пояснения:

Даны условия:

1) \(m > p\) — значит, \(p\) левее \(m\);

2) \(n > m\) — значит, \(n\) правее \(m\);

3) \(n < q\) — значит, \(q\) находится правее \(n\).

Тогда расположение на прямой:

\[ p < m < n

Сравнения:

- \(p\) левее \(n\), значит, \(p < n\);

- \(p\) левее \(q\), значит, \(p < q\);

- \(q\) правее \(m\), значит, \(q > m.\)