Упражнение 746 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник

а) \( x^2-8x+27=\)

\(=(x^2-8x+16)+11=\)

\(=(x-4)^2+11 \)

\((x-4)^2\geq 0\), то наименьшее значение выражения равно 11 при \(x=4\).

Что и требовалось доказать.

б) \( a^2-4a+20=\)

\(=(a^2-4a+4)+16=\)

\(=(a-2)^2+16 \)

\((a-2)^2\geq 0\), то наименьшее значение выражения равно 16 при \(a=2\).

Ответ: наименьшее значение выражения равно 16.

Пояснения:

При выделении полного квадрата трёхчлена мы приводим выражение к виду \((a-b)^2+c\). Квадрат всегда неотрицателен, поэтому минимальное значение достигается тогда, когда квадрат равен нулю, а само выражение равно постоянному слагаемому.

Квадрат разности двух выражений:

\((a - b)^2 = a^2 - 2ab + b^2\).

\(a < b\), \(c > b\), \(c < d\), \(a > e\)

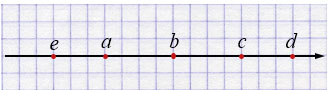
Пояснения:

Чтобы правильно расположить точки на координатной прямой, нужно учесть все данные неравенства.

Даны условия:

1) \(a < b\) — значит, \(a\) левее \(b\);

2) \(c > b\) — значит, \(c\) правее \(b\);

3) \(c < d\) — значит, \(c\) левее \(d\);

4) \(a > e\) — значит, \(a\) правее \(e\).

Итоговый порядок точек на прямой:

\[ e < a < b < c < d. \]