Упражнение 572 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№572 учебника 2023-2025 (стр. 131):
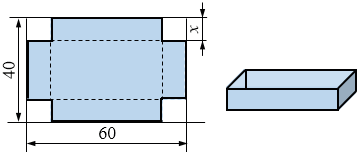
От прямоугольного листа картона, длина которого равна \(60\) см, а ширина - \(40\) см отрезали по углам равные квадраты и из оставшейся части склеили открытую коробку. Найдите сторону квадрата, если площадь основания коробки равна \(800\) см2.
№572 учебника 2013-2022 (стр. 133):
При розыгрыше первенства школы по футболу было сыграно 36 матчей, причём каждая команда сыграла с каждой по одному разу. Сколько команд участвовало в розыгрыше?
Подсказка
№572 учебника 2023-2025 (стр. 131):
Вспомните:
- Что называют квадратом.
- Как найти площадь прямоугольника.
- Решение полных квадратных уравнений (дискриминант).
- Что называют арифметическим квадратным корнем.
- Свойства уравнений.
- Деление и дроби.
- Умножение многочлена на многочлен.
- Противоположные числа.
- Вычитание рациональных чисел.
№572 учебника 2013-2022 (стр. 133):
Вспомните:
- Решение полных квадратных уравнений (дискриминант).
- Что называют арифметическим квадратным корнем.
- Свойства уравнений.
- Деление и дроби.
- Умножение одночлена на многочлен.
- Противоположные числа.
- Вычитание рациональных чисел.
- Умножение рациональных чисел.
- Деление рациональных чисел.
Ответ
№572 учебника 2023-2025 (стр. 131):
Пусть \(x\) см — сторона квадрата, тогда основание коробки имеет размеры \((60-2x)\) см и \((40-2x)\) (см). Площадь основания коробки равна \(800\) см2.
Составим уравнение:
\((60-2x)(40-2x)=800\)
\(2400-120x-80x+4x^2=800\)
\(4x^2-200x+2400-800=0\)
\(4x^2-200x+1600=0\) \( / : 4\)
\(x^2-50x+400=0\)
\(a=1\), \(b=-50\), \(c=400\).
\(D = b^2 - 4ac =\)
\(=(-50)^2-4\cdot1\cdot400=\)
\(=2500-1600=900\) \(\sqrt D=30\).
\(x_1 = \frac{-b + \sqrt{D}}{2a} = \frac{-(-50)+30}{2\cdot1}=\)
\(=\frac{80}{2}=40\) - не удовлетворяет условию.
\(=\frac{20}{2}=10\) - сторона квадрата.
Ответ: сторона квадрата 10 см.
Пояснения:
Площадь прямоугольника:
\(\,S=ab\),
где \(a\) и \(b\) - стороны прямоугольника.
После вырезания по углам квадратов со стороной \(x\) длина и ширина основания уменьшаются на \(2x\), поэтому основание коробки имеет размеры \((60-2x)\) см и \((40-2x)\) (см). Тогда относительно площади можно составить уравнение::
\((60-2x)(40-2x)=800\).
В левой части уравнения, умножив многочлен на многочлен, раскрыли скобки, слагаемое из правой части уравнения перенесли в левую со сменой знака, привели подобные, получили полное квадратное уравнение:
\(4x^2-200x+1600=0\)
Для упрощения разделили обе части уравнения на 4:
\(x^2-50x+400=0\).
Через дискриминант решили полученное уравнение и нашли два корня: 40 и 10. Но сторона квадрата не может быть равна 40 см, так как 40 см сторона коробки. Поэтому искомая сторона квадрата равна 10 см.
№572 учебника 2013-2022 (стр. 133):
Пусть всего было \(x\) команд, тогда каждая команда сыграла \((x-1)\) раз.
Составим уравнение:
\(\dfrac{x(x-1)}{2}=36\) \(/\times2\)
\(x(x-1)=72\)
\(x^2-x-72=0\)
\(a=1\), \(b=-1\), \(c=-72\).
\(D = b^2 - 4ac =\)
\(=(-1)^2 -4\cdot1\cdot(-72)=\)
\(=1+288=289\); \(\sqrt{D}=17\).
\(x_1 = \frac{-b + \sqrt{D}}{2a} =\frac{-(-1)+17}{2\cdot1}=\)
\(=\frac{18}{2}=9\).
\(x_2 = \frac{-b - \sqrt{D}}{2a} =\frac{-(-1)-17}{2\cdot1}=\)
\(=\frac{-16}{2}=-8\) - не удовлетворяет условию \((x>0)\)
Ответ: \(9\) команд.
Пояснения:
Пусть всего было \(x\) команд, тогда каждая команда сыграла \(x-1\) раз. Значит, число матчей равно количеству пар команд:
\(\dfrac{n(n-1)}{2}=36\).
Обе части уравнения домножили на \(2\), раскрыли скобки, слагаемое из правой части уравнения перенесли в левую со сменой знака, получили полное квадратное уравнение:
\(x^2-x-72=0\).
Через дискриминант решили полученное уравнение и нашли два корня. Отрицательный корень не подходит, так как количество команд может быть только натуральным числом. Положительный корень и есть искомое число команд.
Вернуться к содержанию учебника