Упражнение 184 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№184 учебника 2023-2025 (стр. 48):
Обратная пропорциональность задана формулой \(y=\dfrac{10}{x}\).
1) Найдите значение функции, соответствующее значению аргумента, равному \(100\); \(1000\); \(0{,}1\); \(0{,}02\).
2) Определите, принадлежит ли графику этой функции точка \(A(-0{,}05;\,-200)\); \(B(-0{,}1;\,100)\); \(C(400;\,0{,}025)\); \(D(500;\,-0{,}02)\).
№184 учебника 2013-2022 (стр. 47):
На рисунке 6 построен график функции, заданной формулой \(\displaystyle y=\frac{8}{x}\). Найдите по графику:
а) значение \(y\), соответствующее значению \(x\), равному \(2;\;4;\;-1;\;-4;\;-5\);
б) значение \(x\), которому соответствует значение \(y\), равное \(-4;\;-2;\;8\).
Подсказка
№184 учебника 2023-2025 (стр. 48):
Вспомните:
- Функцию обратной пропорциональности.
- Деление и дроби.
- Деление рациональных чисел.
- Деление десятичных дробей.
- Сокращение дробей.
№184 учебника 2013-2022 (стр. 47):
Вспомните:
- График обратной пропорциональности.
- Положение точек на координатной плоскости.
- Перпендикулярные прямые.
- Параллельные прямые.
Ответ
№184 учебника 2023-2025 (стр. 48):
\(y=\dfrac{10}{x}\)
1) Если \(x=100\), то
\( y=\frac{10}{100}=\frac{1}{10}=0{,}1\).
Если \(x=1000\), то
\(y=\frac{10}{1000}=\frac{1}{100}=0{,}01\).
Если \(x=0,1\), то
\(y(0{,}1)=\frac{10}{0{,}1}=100\)
Если \(x=0,02\), то
\(y(0{,}02)=\frac{10}{0{,}02}=\frac{1000}{2}=500. \)
2) \(A(-0{,}05;\,-200)\) - принадлежит графику.
\(-200=\dfrac{10}{-0,05}\)
\(-200=-\dfrac{1000}{-5}\)
\(-200=-200\) - верно.
\(B(-0{,}1;\,100)\) - не принадлежит графику.
\(100=\dfrac{10}{-0,1}\)
\(100=-100\) - неверно.
\(C(400;\,0{,}025)\) - принадлежит графику.
\(0,025=\dfrac{10}{400}\)
\(0,025=\dfrac{1}{40}\)
\(0,025=0,025\) - верно.
\(D(500;\,-0{,}02)\) - не принадлежит графику.
\(-0,02=\dfrac{1}{500}\)
\(-0,02=0,02\) - неверно.
Пояснения:
Использованные правила и приёмы:
• Формула обратной пропорциональности: \(\displaystyle y = \frac{k}{x},\) где \(k\) — постоянная.
• Для вычисления значений функции подставляем заданные \(x\) в формулу \(y=\frac{10}{x}\) и выполняем деление.
• Точка принадлежит графику функции, если при подстановке ее координат в формулу этой функции получается верное равенство.
№184 учебника 2013-2022 (стр. 47):
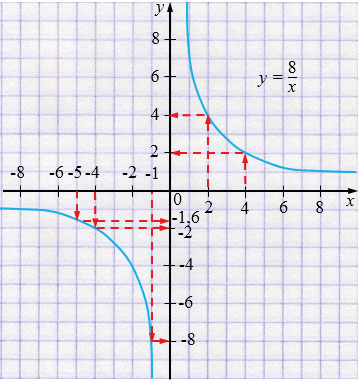
а) Если \(x=2\), то \( y=4\).
Если \(x=4\), то \(y=2\).
Если \(x=-1\), то \(y=-8\).
Если \(x=-4\), то \(y=-2\).
Если \(x=-5\), то \(y=-1,6. \)
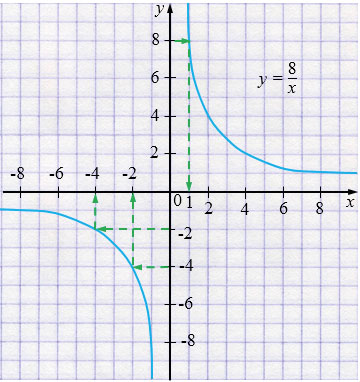
б) Если \(y = -4\), то \(x=-2\).
Если \(y=-2\),то \(x=-4\).
Если \(y=8\), то \(x=1. \)
Пояснения:
а) Чтобы определить по графику значения \(y\) при заданных значениях переменных \(x\), нужно через заданные значения \(x\) провести прямые перпендикулярные к оси \(x\) до пересечения с графиком и через точку на графике провести прямую, параллельную оси \(x\), которая пересечет ось \(y\) в нужной нам точке.
б) Чтобы определить по графику значения \(x\) при заданных значениях переменных \(y\), нужно через заданные значения \(y\) провести прямые параллельные оси \(x\) до пересечения с графиком и через точку на графике провести прямую, перпендикулярную оси \(x\), которая пересечет ось \(x\) в нужной нам точке.
Вернуться к содержанию учебника