Упражнение 681 - ГДЗ Алгебра 7 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№681 учебника 2023-2025 (стр. 145):
(Для работы в парах.) Докажите, что:
а) \(7^8 - 7^7 + 7^6\) делится на 43;
б) \(2^{13} - 2^{10} - 2^9\) делится на 13;
в) \(27^4 - 9^5 + 3^9\) делится на 25;
г) \(16^4 - 2^{13} - 4^5\) делится на 110.
1) Распределите, кто выполняет задания а), в), а кто — задания б), г), и выполните их.
2) Проверьте друг у друга правильность выполнения заданий и исправьте ошибки, если они допущены.
3) Обсудите, какие свойства делимости использованы при выполнении задания.
№681 учебника 2013-2022 (стр. 147):
Выполните умножение:
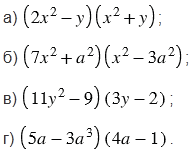
Подсказка
№681 учебника 2023-2025 (стр. 145):
№681 учебника 2013-2022 (стр. 147):
Вспомните:
- Что называют многочленом.
- Умножение многочлена на многочлен.
- Умножение рациональных чисел.
- Подобные слагаемые.
- Сложение рациональных чисел.
- Вычитание рациональных чисел.
- Степень с натуральным показателем.
- Свойства степени с натуральным показателем.
Ответ
№681 учебника 2023-2025 (стр. 145):
а) \(7^8 - 7^7 + 7^6 =\)
\(=7^6\bigl(7^2 - 7 + 1\bigr) = 7^6 \cdot 43\), значит, выражение делится на 43.
б) \(2^{13} - 2^{10} - 2^9 =\)
\(=2^9\bigl(2^4 - 2^1 - 1\bigr) = 2^9 \cdot 13\), значит, выражение делится на 13.
в) \(27^4 - 9^5 + 3^9 =\)
\(=(3^3)^4 - (3^2)^5 + 3^9 =\)
\(=3^{12} - 3^{10} + 3^9 =\)
\(=3^9\bigl(3^3 - 3^1 + 1\bigr) = 3^9 \cdot 25\), значит, выражение делится на 25.
г) \(16^4 - 2^{13} - 4^5 =\)
\(=(2^4)^4 - 2^{13} - (2^2)^5 =\)
\(=2^{16} - 2^{13} - 2^{10} =\)
\(=2^{10}\bigl(2^6 - 2^3 - 1\bigr) = 2^{10} \cdot 55 =\)
\(=2^{10} \cdot 5 \cdot 11=2^{9} \cdot 110\), значит, выражение делится на 110.
Пояснения:
Использованные правила и приёмы:
1) Вынос общего множителя: \[A^n \pm A^m = A^{\min(n,m)}\bigl(A^{|n-m|} \pm 1\bigr).\]
2) Свойство нулевого члена: если выражение равно произведению, то его делимость проверяется делимостью каждого множителя.
3) Критерий делимости: произведение чисел делится на заданное число, если в разложении произведения на простые множители содержатся все простые множители делителя с не меньшими степенями.
В подзадаче а) вынесли \(7^6\) и получили множитель 43.
В подзадаче б) вынесли \(2^9\) и получили множитель 13.
В подзадаче в) перевели все степени к основанию 3, вынесли \(3^9\) и получили множитель 25.
В подзадаче г) перевели все степени к основанию 2, вынесли \(2^{10}\) и получили множитель \(55=5\cdot11\), что вместе с оставшимся \(2^{10}\) содержит в себе \(2\cdot5\cdot11=110\).
№681 учебника 2013-2022 (стр. 147):
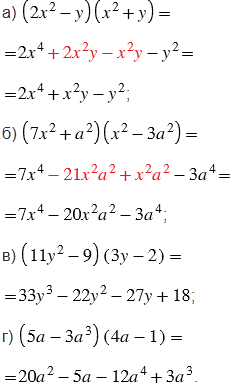
Пояснения:
Чтобы представить выражение в виде многочлена, нужно выполнить умножение многочлена на многочлен.
Чтобы умножить многочлен на многочлен, можно каждый член одного многочлена умножить на каждый член другого и полученные произведения сложить (мы говорим об алгебраической сумме - выражение, которое можно представить в виде суммы положительных и отрицательных чисел). В решении выделены одинаковым цветом подобные слагаемые, их мы складываем (вычитаем), тем самым упрощая выражение.
Также, выполняя умножение многочлена на многочлен, помним, что при умножении степеней с одинаковыми основаниями показатели степени складывают, а основание оставляют тем же.
Вернуться к содержанию учебника