Упражнение 774 - ГДЗ Алгебра 7 класс. Макарычев, Миндюк. Учебник

\(1\tfrac{1}{4}\text{ ч} = 1,25\text{ ч}\)

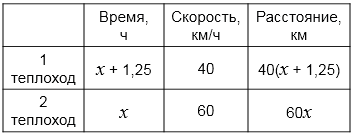
Составим уравнение:

\( 60x = 40\,(x + 1{,}25) \)

\( 60x = 40x + 50 \)

\( 60x - 40x = 50 \)

\( 20x = 50 \)

\( x = \tfrac{50}{20}\)

\( x = 2{,}5\text{ (ч)} \) - был в пути второй теплоход.

\( 60x = 60 \cdot 2{,}5 = 150\text{ (км)} \) - расстояние до пристани.

Ответ: второй теплоход догонит первый через 2,5 ч после своего выхода на расстоянии 150 км от пристани.

Пояснения:

Использованные правила и приёмы:

1. Формула движения: \(S = v\,t\) - чтобы найти расстояние, нужно скорость умножить на время.

2. Учёт запаздывания старта второго теплохода: первый идёт на \(1,25\) ч дольше.

3. Составление уравнения, учитывая то, что расстояние теплоходы пройдут одинаковое, так как отъезжали они от одной пристани.

4. Раскрытие скобок:

\(a(b + c) = ab + ac\),

\(a(b - c) = ab - ac\).

5. Перенос подобных членов из одной части уравнения в другую со сменой знака.

\(A + C= B + D\), то

\(A - D = B - C\).

6. Приведение подобных членов

\(ka + la = (k + l)a\).

7. Решение линейного уравнения, учитывая то, что из линейного уравнения \(ax = b\) следует \(x = \tfrac{b}{a}\) при \(a\neq0\).

Пояснения по шагам:

– Ввели \(x\) как время хода второго теплохода до встречи.

– Выразили путь первого как

\(40(x+1{,}25)\) и второго как \(60x\).

– Составили уравнение

\(60x=40(x+1{,}25)\),

упростили, решили линейное уравнение и получили \(x=2{,}5\) ч.

– Подсчитали расстояние:

\(60\cdot2{,}5=150\) км от пристани A.

\( a + a^2 = a(a + 1). \)

Так как \(a\) и \(a+1\) — два последовательных целых числа, одно из них обязательно чётно, следовательно их произведение делится на 2.

Пояснения:

1. Разложение на множители:

\( a + a^2 =1\cdot{a} + a\cdot{a}=\)

\(=a(1 + a) = a(a+1). \)

2. Свойство последовательных целых: среди любых двух подряд идущих целых чисел одно чётное.

3. Правило делимости произведения: если один из множителей произведения делится на 2, то и всё произведение делится на 2.

Из этого следует, что выражение \(a(a+1)\) всегда чётно, а значит и исходная сумма чётна.