Задание 2.446 - ГДЗ Математика 6 класс. Виленкин, Жохов. Учебник часть 1
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№2.446 учебника 2023-2024 (стр. 103):
Задания олимпиады по математике распечатывали на трех принтерах. На первом принтере распечатали 35% всех заданий, а на втором принтере - 25% всех заданий. Сколько заданий распечатали на третьем принтере, если всего было 240 заданий?
№2.446 учебника 2021-2022 (стр. 98):
Найдите значение выражения:
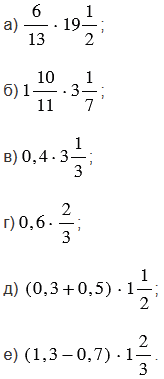
Подсказка
№2.446 учебника 2023-2024 (стр. 103):
Вспомните:
- Проценты.
- Десятичные дроби.
- Деление десятичных дробей.
- Умножение десятичных дробей.
№2.446 учебника 2021-2022 (стр. 98):
Вспомните:
- Умножение обыкновенных дробей.
- Смешанные числа, действия с ними.
- Неправильные дроби.
- Десятичная запись дробных чисел.
- Сложение и вычитание десятичных дробей.
- Сокращение дробей.
- Деление и дроби.
- Деление с остатком.
Ответ
№2.446 учебника 2023-2024 (стр. 103):
1) 35% = 0,35
240 • 0,35 = 84 (з.) - распечатали на первом принтере.
| × | 2 | 4 | 0 | ||
| 0 | 3 | 5 | |||
| + | 1 | 2 | 0 | ||
| 7 | 2 | ||||
| 8 | 4 | 0 | 0 |
2) 25% = 0,25
240 • 0,25 = 60 (з.) - распечатали на втором принтере.
| × | 2 | 4 | 0 | ||
| 0 | 2 | 5 | |||
| + | 1 | 2 | 0 | ||
| 4 | 8 | ||||
| 6 | 0 | 0 | 0 |
3) 240 - (84 + 60) = 240 - 144 = 96 (з.)
Ответ: 96 заданий распечатали на третьем принтере.
Пояснения:
Чтобы найти несколько процентов от числа, нужно сначала перевести проценты в десятичную дробь, а затем умножить число на полученную десятичную дробь. Чтобы проценты записать в виде десятичной дроби, нужно число стоящее перед знаком % разделить на 100.
Всего было 240 заданий, на первом принтере распечатали 35% всех заданий.
35% = 35 : 100 = 0,35.
Значит, на первом принтере распечатали:
240 • 0,35 = 84 (з.).
Всего было 240 заданий, на втором принтере распечатали 25% всех заданий.
25% = 25 : 100 = 0,25.
Значит, на втором принтере распечатали:
240 • 0,25 = 60 (з).
Итак, всего было 240 заданий, из которых 85 заданий распечатали на первом принтере, 60 заданий - на втором принтере, остальные задания распечатали на третьем принтере, значит, на третьем принтере распечатали:
240 - (84 + 60) = 240 - 144 = 96 (з.)
№2.446 учебника 2021-2022 (стр. 98):
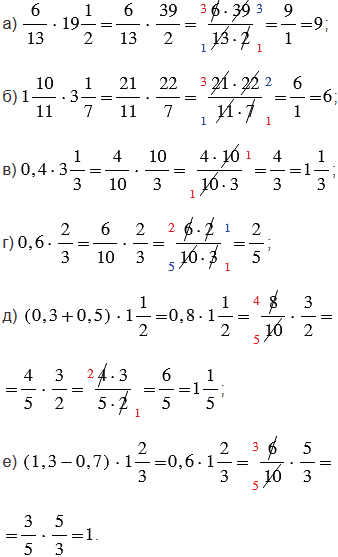
Пояснения:
Правила, по которым выполнены вычисления:
1) произведением двух дробей является дробь, числитель которой равен произведению числителей, а знаменатель - произведению знаменателей. При выполнении умножения дробей, чтобы вычисления были проще, не надо перемножать сразу, лучше сделать это после сокращения. Сократить дробь - значит, разделить ее числитель и знаменатель на одно и то же число (наибольший общий делитель). ;
2) чтобы выполнить умножение смешанных чисел, нужно записать эти числа в виде неправильных дробей, а затем воспользоваться правилом умножения дробей. Чтобы преобразовать смешанное число в неправильную дробь, надо целую часть числа умножить на знаменатель дробной части и к полученному произведению прибавить числитель дробной части; эту сумму записать как числитель неправильной дроби, а в ее знаменатель записать знаменатель дробной части смешанного числа;
3) произведение взаимно обратных чисел равно единице (обратным числу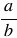 
является число 
).
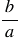Чтобы выполнить умножение десятичных дробей, преобразуем десятичные дроби в обыкновенные дроби, при этом помним, количество знаков после запятой у десятичной дроби совпадает с количеством нулей в знаменателе обыкновенной дроби и, если возможно, полученную обыкновенную дробь сокращаем.
В пунктах д) и е) сначала выполняем действия в скобках, а затем за скобками.
Вернуться к содержанию учебника