Задание 2.122 - ГДЗ Математика 6 класс. Виленкин, Жохов. Учебник часть 1
Старая и новая редакции
Вернуться к содержанию учебника
Выберите год учебника
Вопрос
№2.122 учебника 2023-2024 (стр. 58):
Масса трех космических станций "Салют - 1" (запуск в 1971 г.), "Мир" (запуск в 1986 г.) и МКС (запуск в 1998 г.) равна 560,53 т. Найдите массу каждой станции, если масса станции "Мир" на 105,44 т больше массы станции "Салют - 1", а масса МКС больше массы станции Мир на 292,95 т.
№2.122 учебника 2021-2022 (стр. 52):
Развивай мышление. а) Найдите в таблице простых чисел пары чисел-близнецов среди первых 500 натуральных чисел. Сколько таких пар получилось?
б) Все пары чисел-близнецов, кроме 3 и 5, имеют вид 6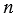
- 1 или 6 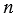+ 1. Найдите по этим выражениям пары чисел для 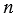, равного 87, 135 и 165. Проверьте, какие из них взаимно простые.
Подсказка
№2.122 учебника 2023-2024 (стр. 58):
Вспомните:
- Что называют уравнением, его корни.
- Сложение и вычитание десятичных дробей.
- Деление десятичных дробей.
№2.122 учебника 2021-2022 (стр. 52):
Вспомните:
- Простые числа.
- Числовые и буквенные выражения.
- Умножение чисел.
- Какие числа называют взаимно простыми.
Ответ
№2.122 учебника 2023-2024 (стр. 58):
Пусть масса станции "Салют - 1" равна 
т, значит, масса станции "Мир" равна
( + 105,44) т, а масса МКС равна
( + 105,44 + 292,95) т.
Масса трех станций 560,53 т.
Составим уравнение:
+ ( + 105,44) + ( + 105,44 +
+ 292,95) = 560,53
( + + ) + (105,44 + 105,44 +
+ 292,95) = 560,53
3 + (210,88 + 291,95) = 560,53
3 + 503,83 = 560,53
3 = 560,53 - 503,83
3 = 56,7
= 56,7 : 3
= 18,9 (т) - масса станции "Салют-1".
|
|
|
+ 105,44 = 18,9 + 105,44 = 124,34 (т) - масса станции "Мир".
| + | 1 | 0 | 5 | , | 4 | 4 |
| 1 | 8 | , | 9 | 0 | ||
| 1 | 2 | 4 | , | 3 | 4 |
+ 105,44 + 292,95 =
= 18,9 + 105,44 + 292,95 =
= 124,34 + 292,95 = 417,29 (т) - масса станции МКС.
| + | 1 | 2 | 4 | , | 3 | 4 |
| 2 | 9 | 2 | , | 9 | 5 | |
| 4 | 1 | 7 | , | 2 | 9 |
Ответ: 18,9 т; 124,34 т и 417,29 т.
Пояснения:
Решаем задачу с помощью уравнения.
Пусть масса станции "Салют - 1" равна т. Масса станции "Мир" на 105,44 т больше массы станции "Салют - 1", а масса МКС больше массы станции Мир на 292,95 т, значит, масса станции "Мир" равна ( + 105,44) т, а масса станции МКС - ( + 105,44 + 292,95) т. Масса трех станций вместе 560,53 т. Получается, можем составить следующее уравнение:
+ ( + 105,44) + ( + 105,44 +
+ 292,95) = 560,53.
Используя сочетательное свойство сложения и распределительное свойство умножения относительно сложения, получим:
( + + ) + (105,44 + 105,44 +
+ 292,95) = 560,53,
3 + (210,88 + 291,95) = 560,53,
3 + 503,83 = 560,53.
Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое, тогда:
3 = 560,53 - 503,83,
3 = 56,7.
Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель, тогда:
= 56,7 : 3,
= 18,9.
Учитывая обозначения введенные выше, масса станции "Салют - 1" равна 18,9 т, масса станции "Мир" равна
+ 105,44 = 18,9 + 105,44 = 124,34 (т),
а масса МКС равна
+ 105,44 + 292,95 =
= 18,9 + 105,44 + 292,95 =
= 124,34 + 292,95 = 417,29 (т).
№2.122 учебника 2021-2022 (стр. 52):
а) 3 и 5; 5 и 7; 11 и 13; 17 и 19; 29 и 31; 41 и 43; 59 и 61; 71 и 73; 101 и 103; 107 и 109; 137 и 139; 149 и 151; 179 и 181; 191 и 193; 197 и 199; 227 и 229; 239 и 241; 269 и 271; 281 и 283; 311 и 313; 347 и 349; 419 и 421; 431 и 433; 461 и 463.
Ответ: получилось 24 пары чисел-близнецов.
б) Если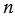 
= 87, то
6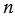 - 1 = 6 • 87 - 1 = 522 - 1 = 521 - простое число.
| × | 8 | 7 |
| 6 | ||
| 5 | 2 | 2 |
6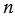 + 1 = 6 • 87 + 1 = 522 + 1 = 523 - простое число.
НОД(521; 523) = 1
Ответ: числа 521 и 523 взаимно простые.
Если 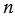= 135, то
6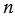 - 1 = 6 • 135 - 1 = 810 - 1 = 809 - простое число.
| × | 1 | 3 | 5 |
| 6 | |||
| 8 | 1 | 0 |
6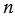 + 1 = 6 • 135 + 1 = 810 + 1 = 811 - простое число.
НОД(809; 811) = 1
Ответ: числа 809 и 811 взаимно простые.
Если 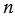= 165, то
6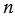 - 1 = 6 • 165 - 1 = 990 - 1 = 989 - составное число.
| × | 1 | 6 | 5 |
| 6 | |||
| 9 | 9 | 0 |
6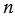 + 1 = 6 • 165 + 1 = 990 + 1 = 991 - простое число.
НОД(989; 991) = 1
Ответ: числа 989 и 991 взаимно простые.
Пояснения:
Натуральное число называют простым, если оно имеет только два натуральных делителя: единицу и само это число.
Два простых числа, разность которых равна 2, называют близнецами.
Натуральные числа называют взаимно простыми, если их наибольший общий делитель равен 1.
Наибольшее натуральное число, на которое делятся нацело каждое из двух данных натуральных чисел, называют наибольшим общим делителем этих чисел.
Наибольший общий делитель простых чисел всегда равен единице.
Наибольший общий делитель составного и простого числа равен единице, если составное число не делится на простое.
Вернуться к содержанию учебника