Площадь прямоугольника / Площадь / Справочник по геометрии 7-9 класс

Площадь прямоугольника

Теорема

Площадь прямоугольника равна произведению его смежных сторон.

Доказательство

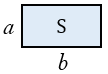
Дано: прямоугольник, 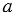, 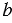- стороны, 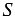- площадь.

Доказать: .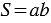

Доказательство:

Достроим прямоугольник до квадрата со стороной .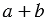

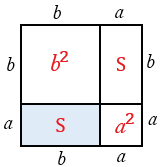
Площадь квадрата равна квадрату его стороны, значит, площадь полученного квадрата равна .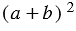

При этом полученный квадрат составлен из данного прямоугольника с площадью 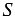, равного ему прямоугольника с площадью 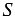(равные многоугольники имеют равные площади) и двух квадратов с площадям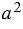и и 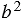(т.к. площадь квадрата равна квадрату его стороны). По свойству 2⁰ площадей, которое говорит о том, что если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников, получаем:

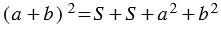или 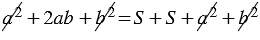, откуда .

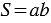Теорема доказана.

Площадь прямоугольника

Доказательство

Советуем посмотреть:

Правило встречается в следующих упражнениях: