Задание 370 - ГДЗ Геометрия 7-9 класс. Атанасян. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№370 учебника 2013-2022 (стр. 100):
Найдите углы выпуклого четырехугольника, если они пропорциональны числам 1, 2, 4, 5.
№370 учебника 2023-2024 (стр. 106):
Подсказка
№370 учебника 2013-2022 (стр. 100):
Вспомните:
- Какой многоугольник называется выпуклым, сумма его углов.
- Какая фигура называется четырехугольником.
№370 учебника 2023-2024 (стр. 106):
Вспомните:
- Свойство касательной к окружности (отрезки касательных).
- Какой треугольник называют прямоугольным.
- Свойства прямоугольного треугольника.
- Перпендикулярные прямые.
Ответ
№370 учебника 2013-2022 (стр. 100):


№370 учебника 2023-2024 (стр. 106):
Дано: 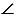 ВАС = 600, В и С точки касания с окр. (О, r), r = 5 см.
ВАС = 600, В и С точки касания с окр. (О, r), r = 5 см.
Найти: ОА.
Решение:
1.  ОАВ =
ОАВ =  ОАС =
ОАС = 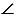 ВАС : 2 = 600 : 2 = 300 (свойство отрезков касательных к окружности).
ВАС : 2 = 600 : 2 = 300 (свойство отрезков касательных к окружности).
2. АВ - касательная, ОВ - радиус, В - точка касания, 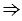 ОВ
ОВ 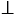 АВ (свойство касательной к окружности),
АВ (свойство касательной к окружности), 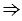
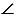 АВО - прямой.
АВО - прямой.
3. 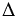 АВО - прямоугольный,
АВО - прямоугольный, 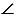 ОАВ = 300,
ОАВ = 300, 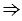 ОА = 2ОВ = 2 • 5 = 10 (см) (свойство прямоугольного треугольника).
ОА = 2ОВ = 2 • 5 = 10 (см) (свойство прямоугольного треугольника).
Ответ: ОА = 10 см.
Пояснения:
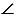 ВАС = 600, тогда
ВАС = 600, тогда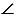 ОАВ =
ОАВ = 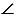 ОАС =
ОАС = 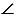 ВАС : 2 = 600 : 2 = 300.
ВАС : 2 = 600 : 2 = 300.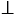 АВ, тогда
АВ, тогда 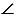 АВО - прямой и
АВО - прямой и 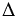 АВО - прямоугольный.
АВО - прямоугольный.Катет прямоугольного треугольника, лежащий против угла в 300, равен половине гипотенузы. В прямоугольном 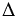 АВО:
АВО:  ОАВ = 300, ОВ = 5 см, тогда
ОАВ = 300, ОВ = 5 см, тогда
ОА = 2ОВ = 2 • 5 = 10 (см)
Вернуться к содержанию учебника