Задание 363 - ГДЗ Геометрия 7-9 класс. Атанасян. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№363 учебника 2013-2022 (стр. 100):
Начертите выпуклые пятиугольник и шестиугольник. В каждом многоугольнике из какой-нибудь вершины проведите все диагонали. Насколько треугольников разделяют проведенные диагонали каждый многоугольник.
№363 учебника 2023-2024 (стр. 105):
Подсказка
№363 учебника 2013-2022 (стр. 100):
Вспомните:
- Какая фигура называется многоугольником.
- Какой многоугольник называется выпуклым.
- Какая фигура называется треугольником.
- Что такое диагональ многоугольника.
№363 учебника 2023-2024 (стр. 105):
Вспомните:
- Что такое окружность.
- Что называют серединным перпендикуляром к отрезку.
Ответ
№363 учебника 2013-2022 (стр. 100):
1) 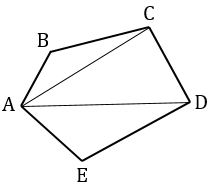
АВСDE - пятиугольник; АС, АD - диагонали, делят АВСDE на 3 треугольника АВС, АСD, АDЕ.
2) 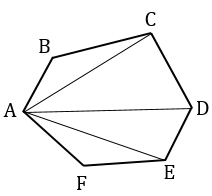
АВСDEF - шестиугольник; АС, АD, АЕ - диагонали, делят АВСDEF на 4 треугольника АВС, АСD, АDЕ, АЕF.
Пояснения:
Пятиугольник - это многоугольник, который имеет 5 вершин и 5 сторон. Диагональ многоугольника - отрезок, соединяющий любые две несоседние вершины, в пятиугольнике АВСDE это отрезки АС и АD, которые разделяют пятиугольник на три треугольника АВС, АСD, АDЕ.
Шестиугольник - это многоугольник, который имеет 6 вершин и 6 сторон. В шестиугольнике АВСDEF диагоналями являются отрезки АС, АD и АЕ, которые разделяют шестиугольник на четыре треугольника АВС, АСD, АDЕ, АЕF.
№363 учебника 2023-2024 (стр. 105):
Пояснения:
Отметим три точки А, В и С, не лежащие на одной прямой.
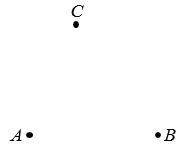
Соединим эти точки отрезками.
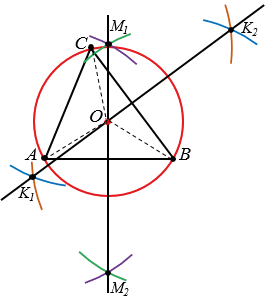
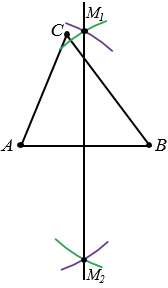
Построим серединный перпендикуляр к отрезку АВ. Построим две окружности с центрами в точках А и B радиуса AB (полностью окружности строить необязательно). Эти окружности пересекутся в двух точках М1 и М2. Проведём прямую М1M2, которая и будет серединным перпендикуляром к отрезку AB.
Аналогично построим серединный перпендикуляр К1К2 к отрезку ВС.
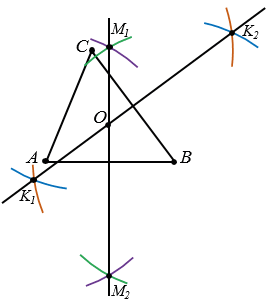
Серединные перпендикуляры М1М2 и K1K2 пересеклись в точке О, которая находится на одинаковом расстоянии от точек А, В и С, т.к. каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка. Поэтому точка О будет центром окружности радиуса ОА = ОВ = ОС, которая пройдет через точки А, В и С. Строим эту окружность.

Вернуться к содержанию учебника