Задание 365 - ГДЗ Геометрия 7-9 класс. Атанасян. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№365 учебника 2013-2022 (стр. 100):
Сколько сторон имеет выпуклый многоугольник, каждый угол которого равен: а) 900; б) 600; в) 1200; г) 1080?
№365 учебника 2023-2024 (стр. 105):
Подсказка
№365 учебника 2013-2022 (стр. 100):
Вспомните:
- Какая фигура называется многоугольником.
- Какой многоугольник называется выпуклым, сумму его углов.
№365 учебника 2023-2024 (стр. 105):
Вспомните:
- Виды треугольников.
- Какая окружность называется вписанной.
- Как построить биссектрису угла.
- Как построить перпендикуляр к прямой, проходящий через точку, не лежащую на данной прямой.
Ответ
№365 учебника 2013-2022 (стр. 100):
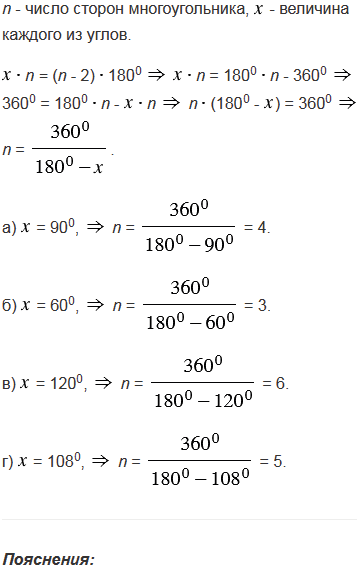

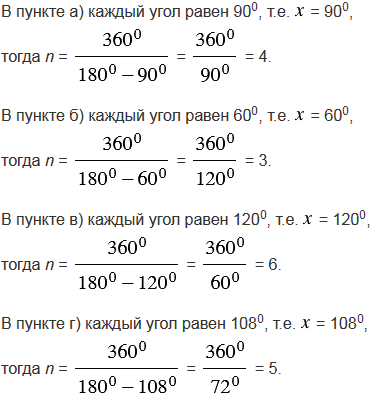
№365 учебника 2023-2024 (стр. 105):
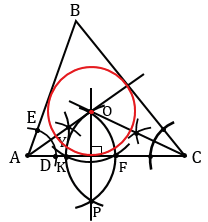
1) Дано:  АВС - остроугольный.
АВС - остроугольный.
Построить: окружность, вписанную в  АВС.
АВС.
Решение:
2) Дано:  АВС - прямоугольный.
АВС - прямоугольный.
Построить: окружность, вписанную в  АВС.
АВС.
Решение:
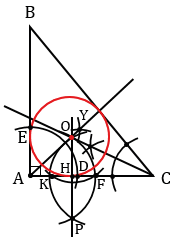
3) Дано:  АВС - тупоугольный.
АВС - тупоугольный.
Построить: окружность, вписанную в  АВС.
АВС.
Решение:
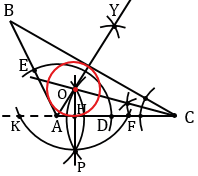
Пояснения:
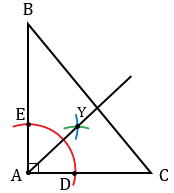
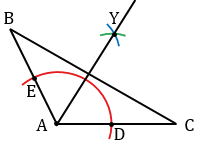
1) Строим остроугольный треугольник АВС.
Центром окружности, вписанной в треугольник является точка пересечения биссектрис этого треугольника. Строим биссектрисы треугольника АВС, три биссектрисы треугольника пересекаются в одной точке, поэтому достаточно построить две из них. Для того чтобы построить биссектрису угла А, с помощью циркуля строим окружность произвольного радиуса с центром в точке А (полностью окружность строить необязательно, смотри выделенное красным цветом). Точки пересечения данной окружности со сторонами АВ и АС обозначаем буквами Е и D. Затем строить две окружности радиуса ЕD с центрами в точках Е и D (полностью окружности строить необязательно, смотри выделенное синим и зеленым цветом). Точку пересечения данных окружностей внутри угла А обозначаем буквой У. Проводим луч АУ, который является биссектрисой угла А.
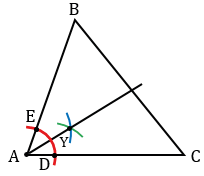
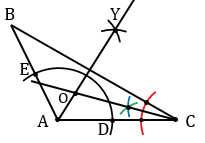
Аналогично биссектрисе угла А строим биссектрису угла С. Точку пересечения биссектрис углов А и С обозначаем буквой О.
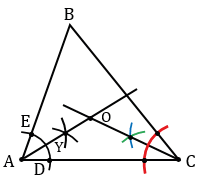
Точка О является центром вписанной окружности. Найдем теперь радиус вписанной окружности. Проведем перпендикуляр из точки О к какой-нибудь из сторон треугольника, например, стороне АС. Для этого строим окружность с центром О так, чтобы она пересекала прямую АС в двух точках (полностью окружность строить необязательно, смотри выделенное красным цветом). Точки пересечения данной окружности с прямой АС обозначим буквами К и F. Затем строим две окружности с центрами в точках К и F, проходящие через точку О (полностью окружности строить необязательно, смотри выделенное синим и зеленым цветом). Точку пересечения данных окружностей обозначим буквой Р. Через точки О и Р проведем прямую, данная прямая будет перпендикулярна к прямой АС, т.е. ОРАС.
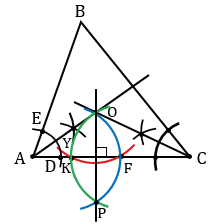
Точку пересечения прямых ОР и АС обозначим буквой Н, отрезок ОН будет радиусом окружности с центром О, вписанной в треугольник АВС. С помощью циркуля строим окружность с центром О радиуса ОН.

2) Для того, чтобы построить окружность, вписанную в прямоугольный треугольник АВС, выполняем все действия, которые выполняли при построении вписанной окружности в остроугольный треугольник (пункт 1).
Строим прямоугольный треугольник АВС.
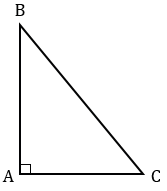
Проводим биссектрису угла А (смотри п.1).
Строим биссектрису угла В (смотри п.1).
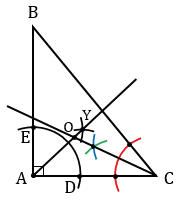
Строим прямую, перпендикулярную прямой АС и проходящую через точку О (смотри п.1).
С помощью циркуля строим окружность с центром О радиуса ОН, которая будет искомой окружностью.

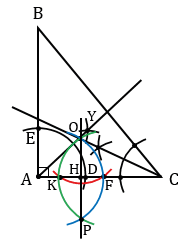
3) Для того, чтобы построить окружность, вписанную в тупоугольный треугольник АВС, выполняем все действия, которые выполняли при построении вписанной окружности в остроугольный треугольник (пункт 1).
Строим тупоугольный треугольник АВС.
Проводим биссектрису угла А (смотри п.1).
Строим биссектрису угла В (смотри п.1).
Строим прямую, перпендикулярную прямой АС и проходящую через точку О (смотри п.1).
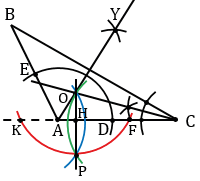
С помощью циркуля строим окружность с центром О радиуса ОН, которая будет искомой окружностью.

Вернуться к содержанию учебника