Задание 339 - ГДЗ Геометрия 7-9 класс. Атанасян. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№339 учебника 2013-2022 (стр. 93):
Отрезок ВВ1 - биссектриса треугольника АВС. Докажите, что ВА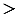 В1А и ВС
В1А и ВС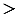 В1С.
В1С.
№339 учебника 2023-2024 (стр. 103):
Подсказка
№339 учебника 2013-2022 (стр. 93):
Вспомните:
- Какая фигура называется треугольником.
- Что такое биссектриса треугольника.
- Какой угол называется внешним углом треугольника.
- Теорему о соотношениях между сторонами и углами треугольника.
№339 учебника 2023-2024 (стр. 103):
Вспомните:
- Что называют окружностью, ее диаметр.
- Какой угол называют острым.
- Внешний угол треугольника, его свойство.
Ответ
№339 учебника 2013-2022 (стр. 93):
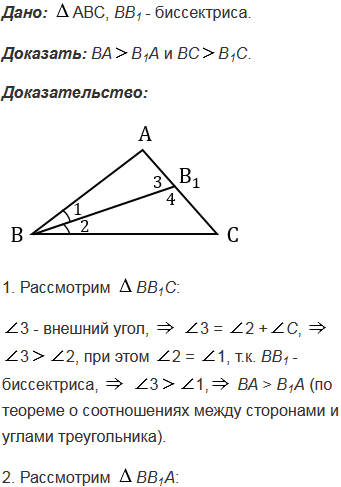



№339 учебника 2023-2024 (стр. 103):
Дано: окружность с центром О, АВ - ее диаметр, точка С лежит вне окружности и С 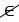 АВ.
АВ.
Д - ть:  АСВ - острый.
АСВ - острый.
Д - во:
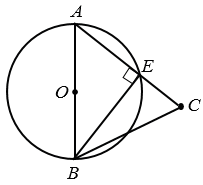
 АЕВ = 900 (свойство диаметра).
АЕВ = 900 (свойство диаметра).
 АЕВ - внешний угол
АЕВ - внешний угол 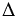 ВЕС,
ВЕС, 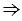
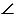 АЕВ =
АЕВ = 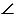 ЕСВ +
ЕСВ + 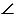 ЕВС = 900,
ЕВС = 900, 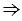
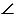 ЕСВ < 900,
ЕСВ < 900, 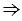
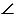 АСВ < 900, т.е.
АСВ < 900, т.е.
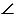 АСВ - острый.
АСВ - острый.
Пояснения:
Из каждой точки окружности любой диаметр, не проходящий через данную точку, виден под прямым углом, следовательно, 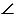 АЕВ - прямой, т.е.
АЕВ - прямой, т.е.
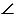 АЕВ = 900.
АЕВ = 900.
Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.
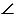 АЕВ - внешний угол
АЕВ - внешний угол 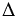 ВЕС, значит,
ВЕС, значит, 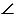 АЕВ =
АЕВ = 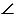 ЕСВ +
ЕСВ + 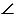 ЕВС = 900, поэтому
ЕВС = 900, поэтому 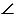 ЕСВ < 900, значит, и
ЕСВ < 900, значит, и 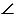 АСВ < 900, так как это один и тот же угол, следовательно,
АСВ < 900, так как это один и тот же угол, следовательно, 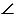 АСВ - острый, т.к. острый угол - это угол градусная мера которого меньше 900.
АСВ - острый, т.к. острый угол - это угол градусная мера которого меньше 900.
Вернуться к содержанию учебника