Задание 345 - ГДЗ Геометрия 7-9 класс. Атанасян. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№345 учебника 2013-2022 (стр. 93):
Через вершину А треугольника АВС проведена прямая, перпендикулярная к биссектрисе угла А, а из вершины В проведен перпендикуляр ВН к этой прямой. Докажите, что периметр треугольника ВСН больше периметра треугольника АВС.
№345 учебника 2023-2024 (стр. 103):
Подсказка
№345 учебника 2013-2022 (стр. 93):
Вспомните:
- Какая фигура называется треугольником.
- Что такое перпендикуляр к прямой.
- Что такое биссектриса угла.
- Какие углы называются вертикальными и их свойство.
- Кокой угол называется развернутым.
- Первый признак равенства треугольников.
- Что такое периметр треугольника.
№345 учебника 2023-2024 (стр. 103):
Вспомните:
- Теорему о касательной.
- Какие прямые называются параллельными.
- Какие прямые называются перпендикулярными.
Ответ
№345 учебника 2013-2022 (стр. 93):
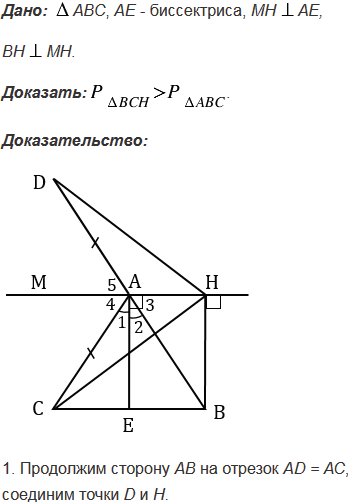





№345 учебника 2023-2024 (стр. 103):
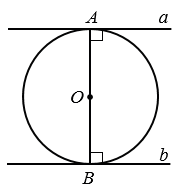
Дано: окружность с центром О, АВ - диаметр, 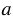 и
и 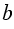 - касательные.
- касательные.
Доказать: 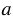
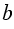
Доказательство:
1. ОА - радиус, 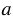 - касательная, А - точка касания,
- касательная, А - точка касания, 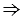 ОА
ОА 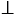
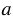 (теорема о касательной),
(теорема о касательной), 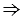 АВ
АВ 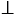
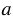 .
.
2. ОВ - радиус, 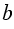 - касательная, В - точка касания,
- касательная, В - точка касания, 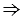 ОB
ОB 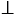
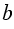 (теорема о касательной),
(теорема о касательной), 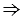 АВ
АВ 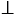
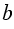 .
.
3. АВ 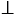
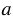 , АВ
, АВ 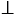
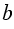 ,
, 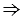
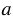
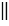
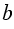 . Что и требовалось доказать.
. Что и требовалось доказать.
Пояснения:
Касательная к окружности перпендикулярна к радиусу, проведённому в точку касания.
ОА - радиус, 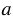 - касательная, А - точка касания, значит, ОА
- касательная, А - точка касания, значит, ОА 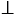
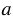 или, учитывая то, что радиус ОА часть диаметра АВ, получаем АВ
или, учитывая то, что радиус ОА часть диаметра АВ, получаем АВ 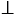
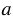 .
.
ОВ - радиус, 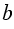 - касательная, значит, В - точка касания, ОB
- касательная, значит, В - точка касания, ОB 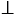
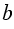 или, учитывая то, что радиус ОВ часть диаметра АВ, получаем АВ
или, учитывая то, что радиус ОВ часть диаметра АВ, получаем АВ 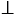
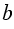 .
.
Итак, АВ 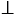
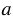 и АВ
и АВ 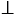
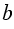 , следовательно,
, следовательно, 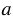
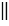
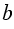 , т.к. две прямые перпендикулярные к третьей прямой друг другу параллельны. Что и требовалось доказать.
, т.к. две прямые перпендикулярные к третьей прямой друг другу параллельны. Что и требовалось доказать.
Вернуться к содержанию учебника