Задание 343 - ГДЗ Геометрия 7-9 класс. Атанасян. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№343 учебника 2013-2022 (стр. 93):
Две стороны треугольника не равны друг другу. Докажите, что медиана, проведенная из их общей вершины, составляет с меньшей из сторон больший угол.
№343 учебника 2023-2024 (стр. 103):
Подсказка
№343 учебника 2013-2022 (стр. 93):
Вспомните:
- Какая фигура называется треугольником.
- Что такое медиана треугольника.
- Какие углы называются вертикальными и их свойство.
- Первый признак равенства треугольников.
- Теорема о соотношениях между сторонами и углами треугольника.
№343 учебника 2023-2024 (стр. 103):
Введите текст
Ответ
№343 учебника 2013-2022 (стр. 93):
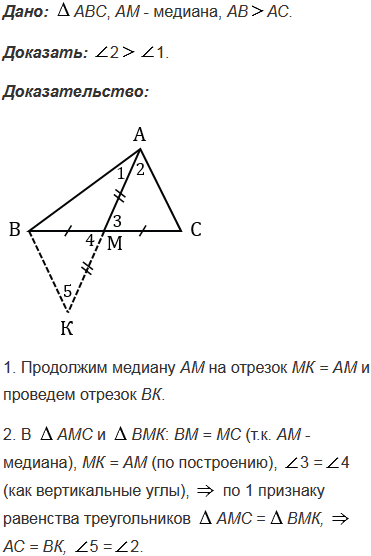
№343 учебника 2023-2024 (стр. 103):
Дано: окр. (О, r); прямая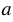 
.
Доказать: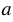 
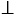r.
Доказательство:
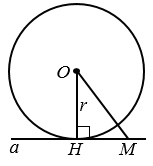
Пусть расстояние от центра О окружности до прямой 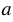равно радиусу r окружности. Опустим из центра О перпендикуляр ОН на прямую 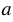. Тогда ОН = r. Для любой другой точки М на прямой 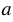наклонная ОМ будет больше перпендикуляра ОН и, следовательно, больше радиуса r. Значит, расстояние от любой точки прямой 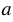, отличной от Н, до центра О больше радиуса r. Поэтому прямая 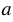и окружность имеют одну общую точку Н, т. е. прямая касается окружности. Что и требовалось доказать.
Вернуться к содержанию учебника