Задание 340 - ГДЗ Геометрия 7-9 класс. Атанасян. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№340 учебника 2013-2022 (стр. 93):
Внутри треугольника АВС взята такая точка D, что АD = АВ. Докажите, что АС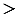 АВ.
АВ.
№340 учебника 2023-2024 (стр. 103):
Подсказка
№340 учебника 2013-2022 (стр. 93):
Вспомните:
- Какая фигура называется треугольником.
- Теорему о соотношениях между сторонами и углами треугольника.
№340 учебника 2023-2024 (стр. 103):
Вспомните:
- Что называют окружностью, ее диаметр и хорды.
- Какие отрезки называют параллельными.
- Какой треугольник называют равнобедренным.
- Свойства равнобедренного треугольника.
- Первый признак равенства треугольников.
- Внешний угол треугольника, его свойство.
Ответ
№340 учебника 2013-2022 (стр. 93):

№340 учебника 2023-2024 (стр. 103):
Дано: окружность с центром О, АВ и СD - хорды, АВ 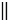 CD, Е и К середины АВ и СD, МN диаметр.
CD, Е и К середины АВ и СD, МN диаметр.
Доказать: Е 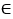 МN и K
МN и K 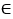 МN.
МN.
Доказательство:
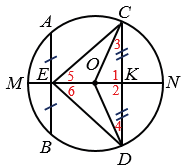
1. Проводим через середину K хорды СD диаметр МN, K
K  МN и МN
МN и МN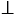 СD и
СD и 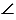 1 =
1 = 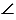 2 = 900.
2 = 900.
Докажем, что Е 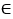 МN.
МN.
2. ОС = ОD - радиусы, 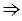
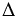 СОD - равнобедренный с основанием СD и
СОD - равнобедренный с основанием СD и 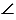 3 =
3 = 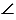 4 (углы при основании).
4 (углы при основании).
3. 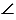 ЕОС и
ЕОС и 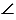 ЕОD - внешние углы
ЕОD - внешние углы 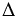 СОK и
СОK и 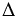 DОK,
DОK, 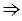
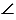 ЕОС =
ЕОС = 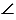 1 +
1 + 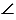 3 и
3 и 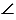 ЕОD =
ЕОD =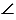 2 +
2 +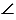 4,
4,
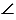 ЕОС =
ЕОС = 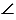 ЕОD (т.к.
ЕОD (т.к.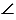 1 =
1 = 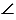 2 и
2 и 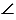 3 =
3 = 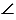 4.
4.
4. В 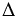 ЕОС и
ЕОС и 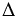 ЕOD: ОС = ОD - радиусы, ЕО - общая,
ЕOD: ОС = ОD - радиусы, ЕО - общая, 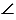 ЕОС =
ЕОС = 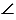 ЕОD,
ЕОD, 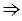
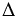 ЕОС =
ЕОС = 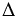 ЕOD по 1 признаку равенства треугольников,
ЕOD по 1 признаку равенства треугольников, 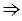 ЕС = ЕD,
ЕС = ЕD, 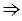
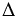 СЕD - равнобедренный с основанием СD.
СЕD - равнобедренный с основанием СD.
5. 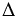 СОD и
СОD и 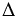 СЕD - равнобедренные с основанием СD,
СЕD - равнобедренные с основанием СD, 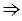 у них высоты лежат на одной прямой,
у них высоты лежат на одной прямой, 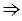 Е
Е 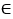 МN, т.к. высота ОК
МN, т.к. высота ОК 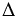 СОD лежит на диаметре МN. Что и требовалось доказать.
СОD лежит на диаметре МN. Что и требовалось доказать.
Пояснения:
При выполнении доказательства мы использовали то, что:
Вернуться к содержанию учебника