Задание 342 - ГДЗ Геометрия 7-9 класс. Атанасян. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№342 учебника 2013-2022 (стр. 93):
Докажите теорему: если в треугольнике биссектриса является медианой, то треугольник равнобедренный.
№342 учебника 2023-2024 (стр. 103):
Подсказка
№342 учебника 2013-2022 (стр. 93):
Вспомните:
- Какой треугольник называется равнобедренным.
- Что такое биссектриса треугольника.
- Что такое медиана треугольника.
- Какие прямые называются параллельными.
- Теорему о накрест лежащих углах.
- Какие углы называются вертикальными и их свойство.
- Второй признак равенства треугольников.
№342 учебника 2023-2024 (стр. 103):
Вспомните:
- Что называют окружностью, ее хорды.
- Что называют расстоянием от точки до прямой.
- Какой треугольник называют равнобедренным.
- Третий признак равенства треугольников.
Ответ
№342 учебника 2013-2022 (стр. 93):
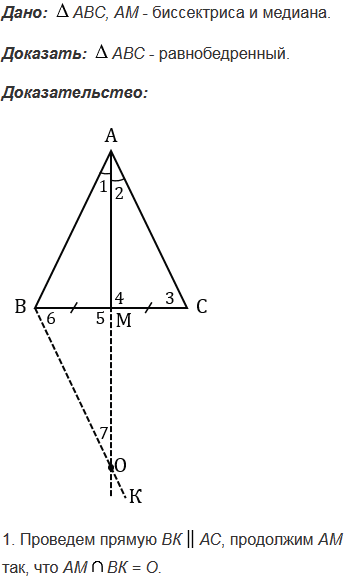




№342 учебника 2023-2024 (стр. 103):
Дано: окружность с центром О, АВ и СD - хорды, ОН = ОК.
Доказать: АВ = СD.
Доказательство:
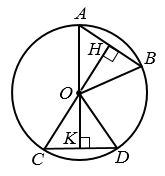
1. Пусть ОН и ОК расстояния от центра окружности точки О до хорд АВ и СD ОН 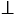 АВ и ОК
АВ и ОК 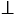 СD,
СD, 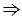 ОН и ОК - высоты равнобедренных треугольников АОВ и СОD (ОА = ОВ = ОС = ОD - радиусы),
ОН и ОК - высоты равнобедренных треугольников АОВ и СОD (ОА = ОВ = ОС = ОD - радиусы), 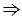 ОН и ОК медианы
ОН и ОК медианы 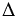 АОВ и
АОВ и 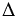 СОD,
СОD, 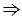 АВ = 2АН и СD = 2СК.
АВ = 2АН и СD = 2СК.
2. В прямоугольных 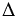 АОН и
АОН и 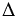 СОК: ОА = ОС - радиусы, ОН = ОК по условию,
СОК: ОА = ОС - радиусы, ОН = ОК по условию, 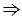
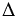 АОН =
АОН = 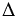 СОК по гипотенузе и катету,
СОК по гипотенузе и катету, 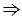 АН = СК,
АН = СК, 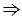 АВ = СD. Что и требовалось доказать.
АВ = СD. Что и требовалось доказать.
Пояснения:
Расстояние от точки до прямой - это длина перпендикуляра (т.е. наименьшее расстояние), проведенного из данной точки к данной прямой. Поэтому, учитывая то, что по построению ОН 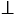 АВ и ОК
АВ и ОК 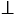 СD, отрезки ОН и ОК - расстояния от центра окружности до хорд АВ и СD соответственно и по условию ОН = ОК.
СD, отрезки ОН и ОК - расстояния от центра окружности до хорд АВ и СD соответственно и по условию ОН = ОК.
Треугольники АОВ и СОD - равнобедренные, так как все радиусы окружности равны, т.е.
ОА = ОВ = ОС = ОD..
ОН 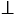 АВ и ОК
АВ и ОК 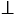 СD, значит, ОН и ОК - высоты равнобедренных треугольников АОВ и СОD. В равнобедренных треугольниках высоты проведенные к основаниям являются и медианами, значит, ОН и ОК медианы треугольников АОВ и СОD. Медиана соединяет вершину треугольника с серединой противолежащей стороны, поэтому АН = ВН и СК = КD, тогда
СD, значит, ОН и ОК - высоты равнобедренных треугольников АОВ и СОD. В равнобедренных треугольниках высоты проведенные к основаниям являются и медианами, значит, ОН и ОК медианы треугольников АОВ и СОD. Медиана соединяет вершину треугольника с серединой противолежащей стороны, поэтому АН = ВН и СК = КD, тогда
АВ = 2АН и СD = 2СК.
В прямоугольных треугольниках АОН и СОК: ОА = ОС - радиусы, ОН = ОК по условию, значит, 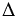 АОН =
АОН = 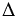 СОК по гипотенузе и катету. В равных треугольниках элементы соответственно равны, тогда АН = СК, а учитывая то, что АВ = 2АН и СD = 2СК, получаем АВ = СD. Что и требовалось доказать.
СОК по гипотенузе и катету. В равных треугольниках элементы соответственно равны, тогда АН = СК, а учитывая то, что АВ = 2АН и СD = 2СК, получаем АВ = СD. Что и требовалось доказать.
Вернуться к содержанию учебника