Задание 346 - ГДЗ Геометрия 7-9 класс. Атанасян. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№346 учебника 2013-2022 (стр. 94):
В треугольнике АВС, где АВ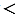 АС, отрезок АD - биссектриса, отрезок АН - высота. Докажите, что точка Н лежит на луче DВ.
АС, отрезок АD - биссектриса, отрезок АН - высота. Докажите, что точка Н лежит на луче DВ.
№346 учебника 2023-2024 (стр. 103):
Подсказка
№346 учебника 2013-2022 (стр. 94):
Вспомните:
- Какая фигура называется треугольником.
- Что такое биссектриса треугольника.
- Что такое высота треугольника.
- Что такое луч.
- Какие углы называются смежными.
- Виды углов.
№346 учебника 2023-2024 (стр. 103):
Вспомните:
- Теорему о касательной.
- Какой треугольник называют прямоугольным.
- Свойства прямоугольных треугольников.
- Какой треугольник называют равнобедренным.
- Признак равнобедренного треугольника.
Ответ
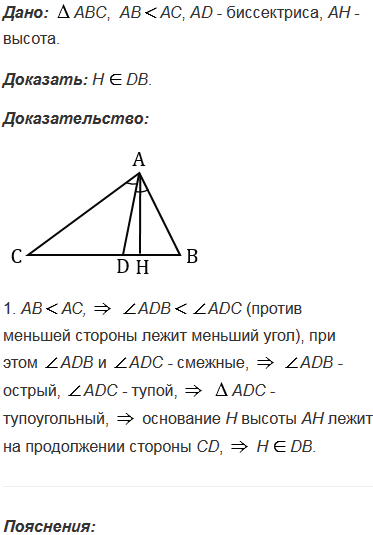
№346 учебника 2013-2022 (стр. 94):

№346 учебника 2023-2024 (стр. 103):
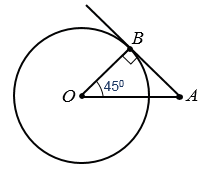
Дано: окружность с центром О, АВ - отрезок касательной, В - точка касания, ОВ = 12 см, 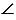 АОВ = 450.
АОВ = 450.
Найти: АВ.
Решение:
ОВ - радиус, АВ - касательная, В - точка касания, 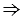 ОВ
ОВ 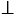 АВ (свойство касательной),
АВ (свойство касательной), 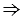
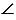 АВО = 900,
АВО = 900, 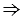
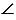 А = 900 -
А = 900 - 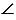 АОВ = 900 - 450 = 450
АОВ = 900 - 450 = 450
(свойство прямоугольного треугольника), 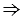
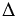 АОВ - равнобедренный с основанием ОА,
АОВ - равнобедренный с основанием ОА, 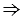 АВ = ОВ = 12 см.
АВ = ОВ = 12 см.
Ответ: АВ = 12 см.
Пояснения:
Касательная к окружности перпендикулярна к радиусу, проведённому в точку касания.
ОВ - радиус окружности, АВ - касательная, В - точка касания, значит, ОВ 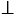 АВ, тогда
АВ, тогда 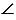 АВО = 900 и
АВО = 900 и 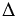 АОВ - прямоугольный.
АОВ - прямоугольный.
В прямоугольном треугольнике сумма острых углов равна 900, поэтому
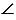 А = 900 -
А = 900 - 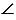 АОВ = 900 - 450 = 450.
АОВ = 900 - 450 = 450.
В 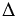 АОВ равны два угла (
АОВ равны два угла (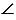 АОВ =
АОВ = 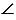 А = 450), значит,
А = 450), значит, 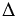 АОВ - равнобедренный с основанием ОА (признак равнобедренного треугольника), следовательно,
АОВ - равнобедренный с основанием ОА (признак равнобедренного треугольника), следовательно,
АВ = ОВ = 12 см.
Вернуться к содержанию учебника