Площадь параллелограмма
Назовем одну из сторон параллелограмма основанием, а перпендикуляр, проведенный из любой точки противоположной стороны к прямой, содержащей основание, - высотой параллелограмма.
Теорема
| Площадь параллелограмма равна произведению его основания на высоту |
Доказательство
Дано: ABCD - параллелограмм, S - площадь ABCD, ВН и СК - высоты
Доказать: S = AD  BH
BH
Доказательство:
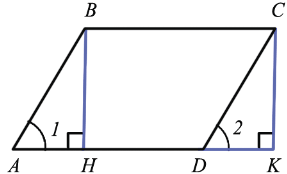
Докажем, что площадь прямоугольника НВСК также равна S. Рассмотрим трапецию АВСК: с одной стороны, она составлена из параллелограмма ABCD и треугольника DCK. Но с другой стороны, она составлена из прямоугольника НВСК и треугольника АВН. Но 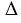 DCK =
DCK = 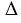 АВН (по гипотенузе (АВ = CD, т.к. они противоположные стороны параллелограмма) и острому углу(углы 1 и 2 как соответственные углы при пересечении параллельных прямых АВ и CD секущей AD)), а равные фигуры имеют равные площади, поэтому их площади равны.
АВН (по гипотенузе (АВ = CD, т.к. они противоположные стороны параллелограмма) и острому углу(углы 1 и 2 как соответственные углы при пересечении параллельных прямых АВ и CD секущей AD)), а равные фигуры имеют равные площади, поэтому их площади равны.
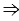 площадь параллелограмма ABCD и прямоугольника НВСК также равны, т.е. площадь прямоугольника НВСК равна S. По теореме площадь прямоугольника равна произведению его смежных сторон, т.е. S = BC
площадь параллелограмма ABCD и прямоугольника НВСК также равны, т.е. площадь прямоугольника НВСК равна S. По теореме площадь прямоугольника равна произведению его смежных сторон, т.е. S = BC  BH, а так как BC = AD, то S = AD
BH, а так как BC = AD, то S = AD  BH. Теорема доказана
BH. Теорема доказана
Советуем посмотреть:
Понятие площади многоугольника
Теорема, обратная теореме Пифагора
Правило встречается в следующих упражнениях:
7 класс
Задание 459, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 464, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 502, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 510, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 526, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 603, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 841, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1021, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1241, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 5, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник