Формула Герона
Теорема
Площадь треугольника 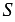 со сторонами со сторонами 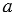 , , 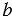 , , 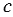 выражается формулой выражается формулой 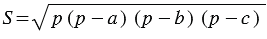 , где , где 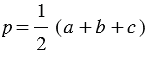 - полупериметр треугольника. - полупериметр треугольника. |
Доказательство
Дано: 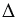 АВС, АВ =
АВС, АВ = 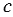 , ВС =
, ВС = 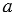 , АС =
, АС = 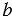 ,
, 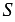 - площадь
- площадь 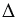 АВС.
АВС.
Доказать: 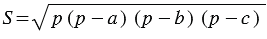 , где
, где 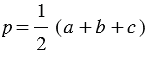 .
.
Доказательство:
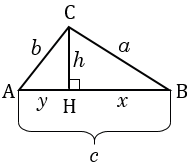
В любом треугольнике по крайней мере два угла острые (свойство треугольника). Пусть в 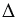 АВС углы А и В - острые. Тогда основание Н высоты СН лежит на стороне АВ. Пусть СН =
АВС углы А и В - острые. Тогда основание Н высоты СН лежит на стороне АВ. Пусть СН =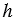 , АН =
, АН =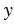 , НВ =
, НВ =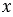 .
.
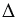 СНВ и
СНВ и  СНА- прямоугольные (т.к. СН - высота), тогда по теореме Пифагора
СНА- прямоугольные (т.к. СН - высота), тогда по теореме Пифагора 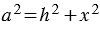 и
и 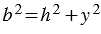 , откуда
, откуда 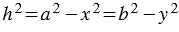 , следовательно,
, следовательно, 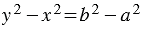 , или
, или 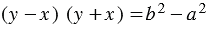 , при этом
, при этом 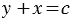 (1), тогда
(1), тогда 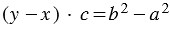 , откуда
, откуда
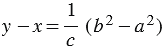 . (2)
. (2)
Сложим равенства (1) и (2), получим:
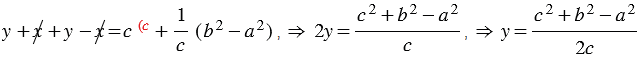 .
.
Поэтому
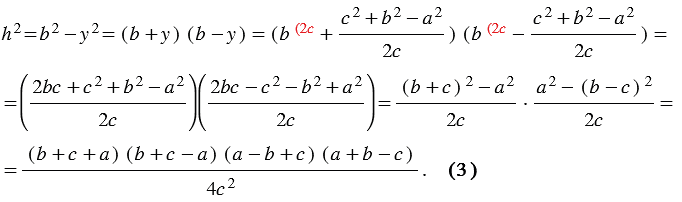
При этом 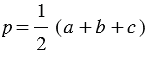 , тогда:
, тогда:
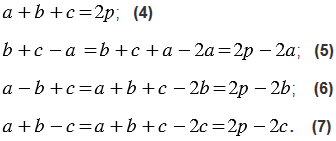
Подставляя выражения (4), (5), (6) и (7) в выражение (3), получим:
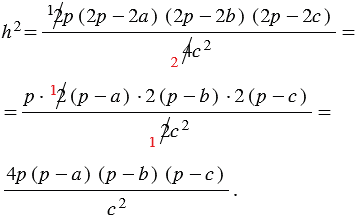
Следовательно, 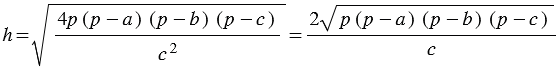 .
.
По формуле площади треугольника: 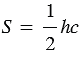 , значит,
, значит,
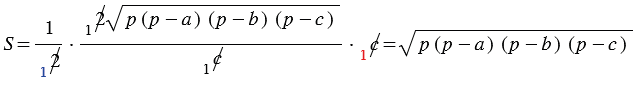 .
.
Теорема доказана.
Полученная формула называется формулой Герона.
Советуем посмотреть:
Понятие площади многоугольника
Теорема, обратная теореме Пифагора
Правило встречается в следующих упражнениях:
7 класс
Задание 525, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 12, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник