Площадь трапеции
Для вычисления площади произвольного многоугольника его разбивают на треугольники и находят площадь каждого из них. Площадь данного многоугольника равна сумме площадей этих треугольников.
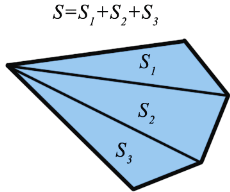
Условимся называть высотой трапеции перпендикуляр, который проведен из любой точки одного из оснований к прямой, содержащей другое основание.
Теорема
| Площадь трапеции равна произведению полусуммы ее оснований на высоту |
Доказательство
Дано: ABCD - трапеция, BH и DH1 - высоты, S - площадь
Доказать: S = 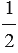 (AD + BC)
(AD + BC)  ВН
ВН
Доказательство:
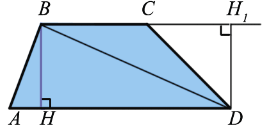
Диагональ BD разделяет трапецию на два треугольника ABD и BCD, поэтому S = SABD + SBCD. Примем отрезки AD и ВН за основание и высоту треугольника ABD, а отрезки BC и DH1 за основание и высоту треугольника BCD. Тогда
SABD = 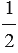 AD
AD  BH, SBCD =
BH, SBCD = 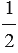 BC
BC  DH1.
DH1.
Так как DH1 = BH, то SBCD = 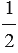 BC
BC  BH.
BH.
Таким образом,
S = 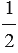 AD
AD  BH +
BH + 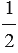 BC
BC  BH =
BH = 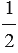 (AD + BC)
(AD + BC)  BH.
BH.
Теорема доказана.
Советуем посмотреть:
Понятие площади многоугольника
Теорема, обратная теореме Пифагора
Правило встречается в следующих упражнениях:
7 класс
Задание 495, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 512, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 518, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 527, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 625, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 725, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 735, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 892, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1070, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 639, Атанасян, Бутузов, Кадомцев, Юдина, Позняк, Учебник