Теорема, обратная теореме Пифагора
Теорема
| Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник прямоугольный. |
Доказательство
Дано: 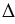 АВС, АВ2 = АС2 + ВС2.
АВС, АВ2 = АС2 + ВС2.
Доказать: 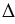 АВС - прямоугольный.
АВС - прямоугольный.
Доказательство:
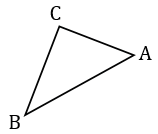
Рассмотрим прямоугольный 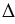 А1В1С1, в котором
А1В1С1, в котором 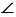 С1 - прямой, А1С1 = АС и В1С1 = ВС.
С1 - прямой, А1С1 = АС и В1С1 = ВС.

По теореме Пифагора А1В12 = А1С12 + В1С12, учитывая то, что А1С1 = АС и В1С1 = ВС, получим, А1В12 = АС2 + ВС2, при этом по условию АВ2 = АС2 + ВС2, значит, А1В12 = АВ2, откуда А1В1 = АВ. Следовательно, 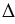 АВС и
АВС и 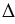 А1В1С1 (по трем сторонам), поэтому
А1В1С1 (по трем сторонам), поэтому 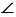 С =
С = 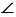 С1, т.е.
С1, т.е. 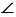 С - прямой, тогда
С - прямой, тогда 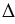 АВС - прямоугольный. Теорема доказана.
АВС - прямоугольный. Теорема доказана.
Пифагоровы треугольники (пифагоровы тройки) - прямоугольные треугольники, у которых длины сторон выражаются целыми числами, которые называют пифагоровы числа. Пифагорова тройка - это три таких натуральных числа (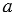 ,
, 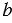 ,
, 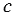 ), для которых справедливо квадратное уравнение:
), для которых справедливо квадратное уравнение: 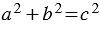 . Так, например, если катеты треугольника равны 6 и 8, а гипотенуза равна 10, то такой треугольник будет пифагоровым, т.к. 62 + 82 = 36 + 64 = 100 = 102, т.е. пифагорова тройка будет: (6, 8, 10).
. Так, например, если катеты треугольника равны 6 и 8, а гипотенуза равна 10, то такой треугольник будет пифагоровым, т.к. 62 + 82 = 36 + 64 = 100 = 102, т.е. пифагорова тройка будет: (6, 8, 10).
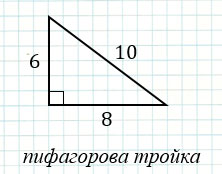
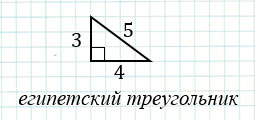
Также, к пифагоровым треугольникам относится треугольник со сторонами 3, 4, 5, который часто называют египетским треугольником, так как он был известен еще древним египтянам.
Советуем посмотреть:
Понятие площади многоугольника
Правило встречается в следующих упражнениях:
7 класс
Задание 498, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 499, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 517, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 524, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 577, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1145, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1241, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1268, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 10, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 11, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник