Упражнение 162 - ГДЗ Алгебра 9 класс. Макарычев, Миндюк. Учебник. Страница 60
Вернуться к содержанию учебника
Вопрос
Покажите схематически, как расположен в координатной плоскости график функции \(y = ax^{2} + bx + c,\; a \ne 0\), если:
1) \(a > 0,\; D > 0;\)
\(a > 0,\; D = 0;\)
\(a > 0,\; D < 0;\)
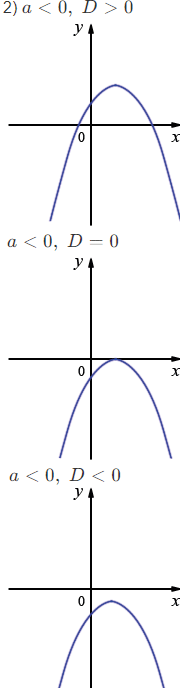
2) \(a < 0,\; D > 0;\)
\(a < 0,\; D = 0;\)
\(a < 0,\; D < 0.\)
(Буквой \(D\) обозначен дискриминант квадратного трёхчлена \(ax^{2} + bx + c\).)
Подсказка
Ответ
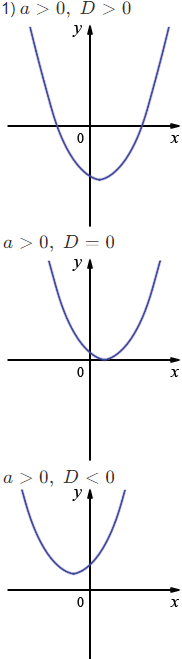
Пояснения:
1. Ветви параболы определяются знаком коэффициента \(a\): если \(a>0\) — ветви направлены вверх, если \(a<0\) — вниз.
2. Количество точек пересечения графика с осью \(Ox\) определяется дискриминантом:
\[ D = b^{2} - 4ac, \] \[ \begin{cases} D>0 & \Rightarrow \text{два пересечения},\\ D=0 & \Rightarrow \text{касание (один корень)},\\ D<0 & \Rightarrow \text{нет пересечений}. \end{cases} \]
3. Совместив знак \(a\) и значение \(D\), можно определить расположение параболы.
Вернуться к содержанию учебника