Упражнение 113 - ГДЗ Алгебра 9 класс. Макарычев, Миндюк. Учебник. Страница 41
Вернуться к содержанию учебника
Вопрос
Используя график функции \(y = x^3\), решите уравнение:
а) \(x^3 = x+1;\)
б) \(x^3 = 2x;\)
в) \(x^3 = 2x + 1.\)
Подсказка
Вспомните:
Ответ
а) \(x^3 = x+1\)
\(y = x^3\)
| \(x\) | -2 | -1 | 0 | 1 | 2 |
| \(y\) | -8 | -1 | 0 | 1 | 8 |
\(y = x+1\)
| \(x\) | \(0\) | \(2\) |
| \(y\) | \(1\) | \(3\) |
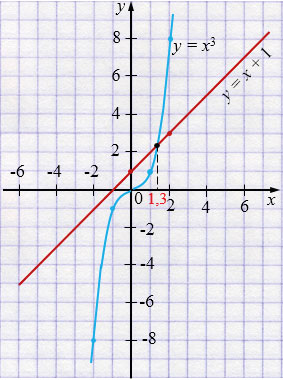
Ответ: \(x \approx 1,3.\)
б) \(x^3 = 2x\)
\(y = x^3\)
| \(x\) | -2 | -1 | 0 | 1 | 2 |
| \(y\) | -8 | -1 | 0 | 1 | 8 |
\(y = 2x\)
| \(x\) | \(0\) | \(2\) |
| \(y\) | \(0\) | \(4\) |

Ответ: \(x \approx 1,4,\) \(x \approx -1,4,\) \(x = 0.\)
в) \(x^3 = 2x + 1\)
\(y = x^3\)
| \(x\) | -2 | -1 | 0 | 1 | 2 |
| \(y\) | -8 | -1 | 0 | 1 | 8 |
\(y = 2x + 1\)
| \(x\) | \(0\) | \(1\) |
| \(y\) | \(1\) | \(3\) |
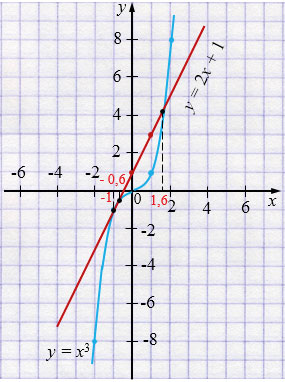
Ответ: \(x \approx 1,6,\) \(x \approx -0,6,\) \(x = 1.\)
Пояснения:
Используем графический способ при решении уравнений. Для этого строим график функции \(y = x^3\) и график линейной функции, стоящей в правой части уравнения. Абсциссы (координаты \(x\) ) точек пересечения этих графиков являются корнями рассматриваемого уравнения.
Вернуться к содержанию учебника