Упражнение 694 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№694 учебника 2023-2025 (стр. 163):
Улитка ползёт по стволу дерева в течение получаса со скоростью \(0{,}25\ \text{м/мин}\). Постройте график движения улитки.
№694 учебника 2013-2022 (стр. 155):
Решите графически уравнение:
а) \(\dfrac{6}{|x|}=1,5x-2\);
б) \(\dfrac{8}{|x|}=x^2\);
в) \(\dfrac{3}{|x|}=x+1\);
г) \(x^2=\dfrac{5}{|x|}\).
Подсказка
№694 учебника 2023-2025 (стр. 163):
Вспомните:
№694 учебника 2013-2022 (стр. 155):
Вспомните:
- Модуль числа.
- График обратной пропорциональности.
- Координаты точки.
- Деление и дроби.
- Деление рациональных чисел.
- Умножение рациональных чисел.
- График квадратичной функции (парабола).
- Степень с натуральным показателем.
- График линейной функции.
- Умножение десятичных дробей.
Ответ
№694 учебника 2023-2025 (стр. 163):
\(t = 30\) (мин) — время.
\(v=0{,}25\) (м/мин) - скорость.
\(s = 0,25\cdot30 = 7,5\) (м) — пройденный путь.
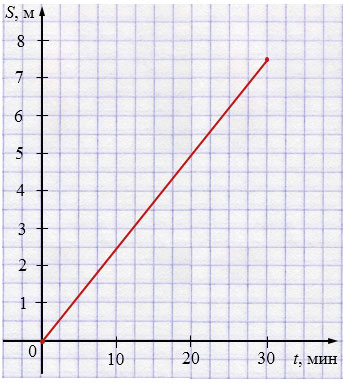
График движения улитки:
\(s=0{,}25\,t\) при \(0\le t\le 30\).
| \(t\) | 0 | 30 |
| \(S\) | 0 | 7,5 |
Пояснения:
Использована формула равномерного движения:
\(s=vt. \)
При постоянной скорости зависимость пути от времени — линейная. Выбираем оси: по горизонтали — время \(t\) (в минутах), по вертикали — путь \(s\) (в метрах). Начальный путь равен нулю, поэтому график проходит через начало координат.
Строим точку \((0;0)\) и точку \((30;7{,}5)\), соединяем их прямой линией. Получаем отрезок графика функции \(s=0{,}25\,t\), определённый на интервале движения \(0\le t\le 30\) минут.
№694 учебника 2013-2022 (стр. 155):
а) \(\dfrac{6}{|x|}=1,5x-2\)
\(y=\dfrac{6}{|x|}\) и \(y = 1,5x-2\)
1) \(y=\dfrac{6}{|x|}\)
Если \(x>0\), то \(y=\dfrac{6}{x}\)
| \(x\) | 1 | 2 | 3 | 6 |
| \(y\) | 6 | 3 | 2 | 1 |
Если \(x<0\), то \(y=-\dfrac{6}{x}\)
| \(x\) | -1 | -2 | -3 | -6 |
| \(y\) | 6 | 3 | 2 | 1 |
2) \(y= 1,5x-2\)
| \(x\) | 0 | 2 |
| \(y\) | -2 | 1 |

Ответ: \(x=2,8.\)
б) \(\dfrac{8}{|x|}=x^2.\)
\(y=\dfrac{8}{|x|}\) и \(y = x^2\)
1) \(y=\dfrac{8}{|x|}\)
Если \(x>0\), то \(y=\dfrac{8}{x}\)
| \(x\) | 1 | 2 | 4 | 8 |
| \(y\) | 8 | 4 | 2 | 1 |
Если \(x<0\), то \(y=-\dfrac{8}{x}\)
| \(x\) | -1 | -2 | -4 | -8 |
| \(y\) | 8 | 4 | 2 | 1 |
2) \(y = x^2\)
| \(x\) | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| \(y\) | 9 | 4 | 1 | 0 | 1 | 4 | 9 |

Ответ: \(x= 2\) и \(x= -2\).
в) \(\dfrac{3}{|x|}=x+1.\)
\(y=\dfrac{3}{|x|}\) и \(y = x+1\)
1) \(y=\dfrac{3}{|x|}\)
Если \(x>0\), то \(y=\dfrac{3}{x}\)
| \(x\) | 0,5 | 1 | 3 | 6 |
| \(y\) | 6 | 3 | 1 | 0,5 |
Если \(x<0\), то \(y=-\dfrac{3}{x}\)
| \(x\) | -0,5 | -1 | -3 | -6 |
| \(y\) | 6 | 3 | 1 | 0,5 |
2) \(y= x+1\)
| \(x\) | 0 | 3 |
| \(y\) | 1 | 4 |

Ответ: \(x=1,2.\)
г) \(x^2=\dfrac{5}{|x|}\)
1) \(y = x^2\)
| \(x\) | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| \(y\) | 9 | 4 | 1 | 0 | 1 | 4 | 9 |
2) \(y=\dfrac{5}{|x|}\)
Если \(x>0\), то \(y=\dfrac{5}{x}\)
| \(x\) | 1 | 2 | 2,5 | 5 |
| \(y\) | 5 | 2,5 | 2 | 1 |
Если \(x<0\), то \(y=-\dfrac{5}{x}\)
| \(x\) | -1 | -2 | -2,5 | -5 |
| \(y\) | 5 | 2,5 | 2 | 1 |

Ответ: \(x=1,8\) и \(x = -1,8\).
Пояснения:
Чтобы решить графически данные уравнения, нужно найти точки пересечения графиков функций, стоящих в левой и правой частях уравнения. Решением уравнения являются значения координаты \(x\) точек пересечения графиков.
Все уравнения содержат модуль, поэтому рассматриваются два случая: \(x>0\) и \(x<0\).
1) \(y = x^2\) - квадратичная функция, графиком которой является парабола. Строят график по точкам (для нескольких положительных и нескольких отрицательных значений \(x\) определяют значения \(y\)).
2) \(y= \frac{k}{|x|}\) - функция обратной пропорциональности.
Если \(x \ge 0\), то \(|x| = x\), тогда
\(y= \frac{k}{x}\) - графиком является ветвь гиперболы, расположенная в I координатной четверти.
Если \(x < 0\), то \(|x| = -x\), тогда
\(y= -\frac{k}{x}\) - графиком является ветвь гиперболы, расположенная во II координатной четверти.
3) \(y = kx + b\) - линейная функция, графиком является прямая. Для построения прямой достаточно двух точек.
Вернуться к содержанию учебника