Упражнение 188 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№188 учебника 2023-2025 (стр. 49):
Постройте график функции:
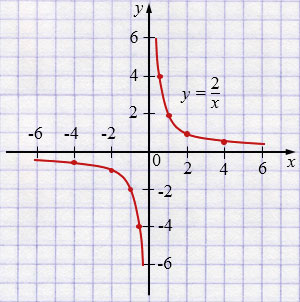
а) \(y=\frac{2}{x}\);
б) \(y=-\frac{2}{x}\);
в) \(y=\frac{3}{x}\);
г) \(y=-\frac{4}{x}\);
д) \(y=\frac{1}{2x}\);
е) \(y=-\frac{2}{5x}\).
№188 учебника 2013-2022 (стр. 47):
(Для работы в парах.) Используя графические представления, выясните, сколько решений имеет уравнение:
а) \(\displaystyle \frac{k}{x}=x^2,\) где \(k>0\);
б) \(\displaystyle \frac{k}{x}=x^2,\) где \(k<0\);
в) \(\displaystyle \frac{k}{x}=x^3,\) где \(k>0\);
г) \(\displaystyle \frac{k}{x}=x^3,\) где \(k<0\).
1) Распределите, кто выполняет задания а) и г), а кто - задания б) и в), и выполните их.
2) Проверьте друг у друга, верно ли построены графики функций \(y = \frac{k}{x}\).
3) Обсудите правильность сделанных выводов о числе решений уравнения.
Подсказка
№188 учебника 2023-2025 (стр. 49):
Вспомните:
- График обратной пропорциональности.
- Положение точек на координатной плоскости.
- Деление и дроби.
- Деление десятичных дробей.
- Деление рациональных чисел.
- Умножение рациональных чисел.
№188 учебника 2013-2022 (стр. 47):
Вспомните:
- График обратной пропорциональности.
- Положение точек на координатной плоскости.
- График квадратичной функции (парабола).
- График кубической параболы.
Ответ
№188 учебника 2023-2025 (стр. 49):
а) \(y=\frac{2}{x}\)
| \(x\) | -4 | -2 | -1 | -0,5 |
| \(y\) | -0,5 | -1 | -2 | -4 |
| \(x\) | 0,5 | 1 | 2 | 4 |
| \(y\) | 4 | 2 | 1 | 0,5 |
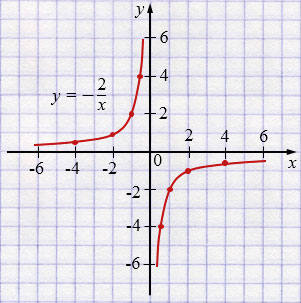
б) \(y=-\frac{2}{x}\)
| \(x\) | -4 | -2 | -1 | -0,5 |
| \(y\) | 0,5 | 1 | 2 | 4 |
| \(x\) | 0,5 | 1 | 2 | 4 |
| \(y\) | -4 | -2 | -1 | -0,5 |
в) \(y=\frac{3}{x}\)
| \(x\) | -6 | -3 | -1 | -0,5 |
| \(y\) | -0,5 | -1 | -3 | -6 |
| \(x\) | 0,5 | 1 | 3 | 6 |
| \(y\) | 6 | 3 | 1 | 0,5 |

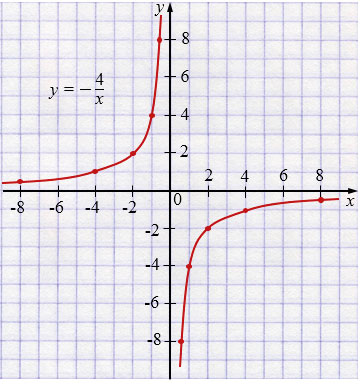
г) \(y=-\frac{4}{x}\)
| \(x\) | -8 | -4 | -2 | -1 | -0,5 |
| \(y\) | 0,5 | 1 | 2 | 4 | 8 |
| \(x\) | 0,5 | 1 | 4 | 2 | 8 |
| \(y\) | -8 | -4 | -1 | -2 | -0,5 |
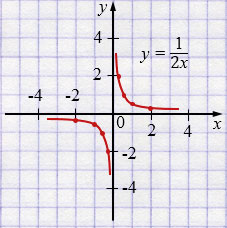
д) \(y=\frac{1}{2x}\)
| \(x\) | -2 | -1 | -0,5 | -0,25 |
| \(y\) | -0,25 | -0,5 | -1 | -2 |
| \(x\) | 2 | 1 | 0,5 | 0,25 |
| \(y\) | 0,25 | 0,5 | 1 | 2 |
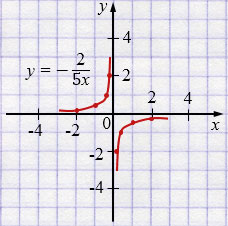
е) \(y=-\frac{2}{5x}\)
| \(x\) | -2 | -1 | -0,4 | -0,2 |
| \(y\) | 0,2 | 0,4 | 1 | 2 |
| \(x\) | 2 | 1 | 0,4 | 0,2 |
| \(y\) | -0,2 | -0,4 | -1 | -2 |
Пояснения:
Использованные правила и приёмы:
Общая форма всех функций: \[ y = \frac{k}{x}, \] где \(k\) - какое-то число.
• Графиком обратной пропорциональности \(y=\frac{k}{x}\) является гипербола (две ветви). Строят график по точкам (для нескольких положительных и нескольких отрицательных значений \(x\) определяют значения \(y\)).
• Знак \(k\) определяет положение ветвей в координатных четвертях:
– Если \(k>0\), то ветви гиперболы лежат в I и III координатных четвертях;
– Если \(k<0\), то ветви гиперболы лежат во II и IV координатных четвертях.
№188 учебника 2013-2022 (стр. 47):
а) \(\displaystyle \frac{k}{x}=x^2,\) где \(k>0\)
\(y=\frac{k}{x}\), где \(k>0\) - гипербола в I и III четвертях.
\(y=x^2\) - парабола в I и II четвертях.

Ответ: одно решение.
б) \(\displaystyle \frac{k}{x}=x^2,\) где \(k<0\)
\(y=\frac{k}{x}\), где \(k<0\) - гипербола во II и IV четвертях.
\(y=x^2\) - парабола в I и II четвертях.

Ответ: одно решение.
в) \(\displaystyle \frac{k}{x}=x^3,\) где \(k>0\)
\(y=\frac{k}{x}\), где \(k>0\) - гипербола в I и III четвертях.
\(y=x^3\) - кубическая парабола в I и III четвертях.

Ответ: два решения.
г) \(\displaystyle \frac{k}{x}=x^3,\) где \(k<0\)
\(y=\frac{k}{x}\), где \(k<0\) - гипербола во II и IV четвертях.
\(y=x^3\) - кубическая парабола в I и III четвертях.

Ответ: решений нет.
Пояснения:
При графическом решении уравнений количество точек пересечения графиков, соответствующих функциям, стоящим в левой и правой частях уравнения, говорит о количестве решений, которое имеет данное уравнение.
Вернуться к содержанию учебника