Упражнение 264 - ГДЗ Алгебра 8 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№264 учебника 2023-2025 (стр. 63):
Постройте график функции:
а) \(y = \dfrac{x^2 - 16}{\lvert x - 4\rvert}\);
б) \(y = \dfrac{x^2 - 25}{5 + \lvert x\rvert}\).
№264 учебника 2013-2022 (стр. 65):
Найдите разность множеств \(A\) и \(B\), если:
а) \(A\) — множество чётных чисел, \(B\) — множество чисел, кратных 3;
б) \(A\) — множество делителей числа 18, \(B\) — множество делителей числа 12;
в) \(A\) — множество треугольников, \(B\) — множество прямоугольных треугольников;
г) \(A\) — множество прямоугольников, \(B\) — множество ромбов.
Подсказка
№264 учебника 2023-2025 (стр. 63):
№264 учебника 2013-2022 (стр. 65):
Вспомните:
- Что называют множеством.
- Делители числа.
- Четные и нечетные числа.
- Треугольники, их виды.
- Прямоугольники.
- Квадраты.
Ответ
№264 учебника 2023-2025 (стр. 63):
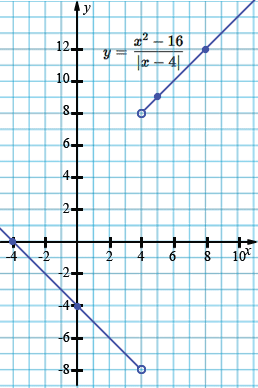
а) \(y = \dfrac{x^2 - 16}{\lvert x - 4\rvert}\);
Область определения:
\(\lvert x - 4\rvert \neq 0\)
\( x \neq 4.\)
При \(x>4\):
\(\lvert x-4\rvert = x-4\),
\(y = \frac{(x-4)(x+4)}{x-4} = x + 4.\)
При \(x<4\):
\(\lvert x-4\rvert = 4 - x\),
\(y = \frac{(x-4)(x+4)}{\,4 - x} =\)
\(=-\,\frac{(x-4)(x+4)}{x-4} =\)
\(=-\,(x + 4).\)
Итого:
\(y = \begin{cases} -\,(x+4), & x<4,\\ x+4, & x>4, \end{cases} \quad x\neq 4. \)
| \(x\) | 0 | -4 | 4 |
| \(y\) | -4 | 0 | -8 |
| \(x\) | 5 | 8 | 4 |
| \(y\) | 9 | 12 | 8 |
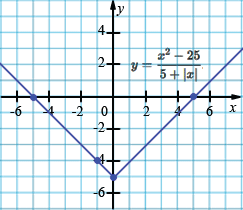
б) \(y = \dfrac{x^2 - 25}{5 + \lvert x\rvert}\).
Область определения:
\(5 + \lvert x\rvert \neq 0\)
\(\lvert x\rvert\neq-5\) верно при любом значении \(x\), \(\Longrightarrow\)область определения: все числа.
При \(x\ge 0\): \(\lvert x\rvert = x\),
\(5+\lvert x\rvert = x+5\),
\(y = \frac{(x-5)(x+5)}{x+5} = x - 5.\)
При \(x<0\): \(\lvert x\rvert = -x\),
\(5+\lvert x\rvert = 5 - x = -(x-5)\),
\(y = \frac{(x-5)(x+5)}{5 - x} =\)
\(=-\,\frac{(x-5)(x+5)}{x-5} =\)
\(=-\,(x + 5)\)
Итого:
\( y = \begin{cases} -\,(x+5), & x<0,\\ x-5, & x\ge 0. \end{cases} \)
| \(x\) | -5 | -1 | 0 | 5 |
| \(y\) | 0 | -4 | -5 | 0 |
Пояснения:
Разность квадратов двух выражений:
\(a^2 - b^2 = (a - b)(a + b)\)
Модуль числа:
\( \lvert u\rvert = \begin{cases} u, & u\ge0,\\ -\,u, & u<0. \end{cases} \)
Особые точки и разрывы:
— В пункте а) при \(x=4\) знаменатель обращается в ноль — точка разрыва (график имеет «дырку»).
— В пункте б) знаменатель никогда не обращается в ноль, график непрерывен на всей оси \(Ox\).
№264 учебника 2013-2022 (стр. 65):
а) \(A\) — множество чётных чисел,
\(B\) — множество чисел, кратных 3.
\((A - B)\) - множество четных чисел, не кратных 3.
б) \(A\) — множество делителей числа 18,
\(B\) — множество делителей числа 12.
\((A - B)\) - множество чисел из \(A\), которых нет в \(B\).
в) \(A\) — множество треугольников,
\(B\) — множество прямоугольных треугольников;
\((A - B)\) - множество остроугольных и тупоугольных треугольников.
г) \(A\) — множество прямоугольников,
\(B\) — множество ромбов.
\((A - B)\) - множество прямоугольников, не являющихся квадратами.
Пояснения:
Разность множеств \((A - B)\) — это множество всех элементов, принадлежащих \(A\), но не принадлежащих \(B\).
В каждом пункте мы исключаем из множества \(A\) те элементы, которые принадлежат множеству \(B\).
Вернуться к содержанию учебника