Понятие множества
| Словом "множество" в математическом языке обозначают любую совокупность объектов или предметов, объединенных каким-либо общим признаком. |
Примеры множеств:
множество месяцев в году, множество материков на планете Земля, множество игроков в футбольной команде, множество коров в стаде и т.д.
Множества как правило обозначают большими буквами латинского алфавита: А, В, С, D, М, N и т.д.
| Элемент множества - каждый объект (предмет), входящий в это множество. |
Например, январь элемент, входящий в множество месяцев в году.
Способы задания множества:
1. Множество задают указанием (перечислением) всех его элементов.
2. Множество задают характеристическими свойствами элементов множества.
Для записи множества с помощью перечисления элементов используют фигурные скобки.
Например, множество дней в неделе записывают так:
{понедельник, вторник, среда, четверг, пятница, суббота воскресенье}.
| Числовое множество - это множество, элементами которого являются числа. |
Например, {1, 3, 5, 7, 9} - множество однозначных нечетных чисел.
Обратите внимание, множество {3, 5, 7} и множество {7, 3, 5} - это одно и то же множество, состоящее из чисел 3, 5 и 7.
Для того, чтобы на математическом языке записать предложение "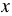 - элемент множества А" (или, то же самое, "
- элемент множества А" (или, то же самое, "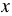 принадлежит множеству А"), используют знак
принадлежит множеству А"), используют знак 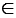 . Соответствующая запись выглядит так:
. Соответствующая запись выглядит так: 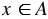 . Также, можно догадаться, что запись "
. Также, можно догадаться, что запись "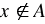 " означает "
" означает "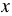 не является элементом множества А".
не является элементом множества А".
Множества бывают конечные и бесконечные.
Конечные множества - это множества, которые содержат конечное число элементов (например, количество учеников одного класса - конечное множество).
Бесконечные множества - это множества, которые содержат бесконечное число элементов (например, множество натуральных чисел).
Также множество может состоять из одного элемента. Например, множество натуральных чисел, расположенных межу числами 99 и 101: {100}.
Бывает такое, что описав словами некоторое множество, нельзя гарантировать, что найдется хотя бы один объект, отвечающий этому описанию. Например, множество А - множество чисел, которые делятся на 9, но не делятся на 3. Таких чисел не существует. Получается, мы описали множество, которое не содержит ни одного элемента - пустое множество. Пустое множество обозначают символом 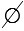 .
.
| Два множества А и В называют равными, если они состоят из одних и тех же элементов, то есть каждый элемент из множества А принадлежит множеству В и наоборот - каждый элемент множества В принадлежит множеству А. |
Если множества А и В равны, то пишут А = В.
Рассмотрим множества {2, 4, 6, 8} и {4; 8}. Каждый элемент второго множества принадлежит также и первому, но не каждый элемент первого множества принадлежит второму множеству. Тогда говорят, что второе множество является подмножеством первого.
| Множество А называют подмножеством множества В, если каждый элемент множества А является элементом множества В. Пустое множество считают подмножеством любого другого множества. |
Если множество А является подмножеством множества В, то в символическом виде это записывают: 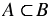 .
.
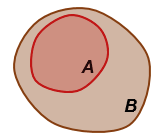
Изобразить то, что 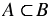 можно следующим образом:
можно следующим образом:
Советуем посмотреть:
Подмножество. Операции над множествами. Объединение и пересечение множеств
Правило встречается в следующих упражнениях:
5 класс
Задание 865, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 869, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 870, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 877, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 887, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 908, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 909, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 1, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 6, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 10, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
6 класс
Задание 7, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 57, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 60, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 55, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 1.134, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 1.140, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 1.161, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 1.163, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 2.39, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 4.26, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
7 класс
Упражнение 1, Макарычев, Миндюк, Нешков, Суворова, Учебник
Упражнение 2, Макарычев, Миндюк, Нешков, Суворова, Учебник
8 класс
Номер 424, Мерзляк, Полонский, Якир, Учебник
Номер 442, Мерзляк, Полонский, Якир, Учебник
Номер 444, Мерзляк, Полонский, Якир, Учебник
Номер 448, Мерзляк, Полонский, Якир, Учебник
Номер 451, Мерзляк, Полонский, Якир, Учебник
Номер 455, Мерзляк, Полонский, Якир, Учебник
Номер 459, Мерзляк, Полонский, Якир, Учебник
Номер 3, Мерзляк, Полонский, Якир, Учебник
Номер 482, Мерзляк, Полонский, Якир, Учебник
Упражнение 264, Макарычев, Миндюк, Учебник