Упражнение 961 - ГДЗ Алгебра 7 класс. Макарычев, Миндюк. Учебник

а) \( x^2 + 2xy + y^2 - m^2 =\)

\(= (x^2 + 2xy + y^2) - m^2 =\)

\(=(x + y)^2 - m^2 =\)

\(=\bigl((x + y) - m\bigr)\,\bigl((x + y) + m\bigr) =\)

\(=(x + y - m)\,(x + y + m). \)

б) \( p^2 - a^2 - 2ab - b^2 =\)

\(=p^2 - \bigl(a^2 + 2ab + b^2\bigr) =\)

\(=p^2 - (a + b)^2 =\)

\(=(p - (a + b))\,(p + (a + b)) = \)

\(=(p - a - b)\,(p + a + b). \)

в) \( b^2 - c^2 - 8b + 16 =\)

\(=(b^2 - 8b + 16) - c^2 = \)

\(=(b - 4)^2 - c^2 =\)

\(=\bigl((b - 4) - c\bigr)\,\bigl((b - 4) + c\bigr) =\)

\(=(b - c - 4)\,(b + c - 4). \)

г) \( 9 - c^2 + a^2 - 6a =\)

\(=(a^2 - 6a + 9) - c^2 =\)

\(=(a - 3)^2 - c^2 =\)

\(=\bigl((a - 3) - c\bigr)\,\bigl((a - 3) + c\bigr) =\)

\(=(a - c - 3)\,(a + c - 3). \)

Пояснения:

Использованные правила и приёмы:

— Формула разности квадратов:

\( a^2 - b^2 = (a - b)\,(a + b). \)

Применялась в каждом пункте, когда выражение представлялось как разность двух квадратов.

— Формула квадрата двучлена:

\(a^2 + 2ab + b^2 = (a + b)^2\) - квадрат суммы;

\(a^2 - 2ab + b^2 = (a - b)^2\) - квадрат разности.

Пояснение к пункту а):

В выражении \(x^2 + 2xy + y^2 - m^2\) сначала заметили полный квадрат \(x^2 + 2xy + y^2 = (x + y)^2\), после чего получили разность квадратов

\((x + y)^2 - m^2\).

По формуле разности квадратов это даёт

\((x + y - m)(x + y + m)\).

Пояснение к пункту б):

В выражении \(p^2 - a^2 - 2ab - b^2\) сгруппировали вторую часть как полный квадрат

\(a^2 + 2ab + b^2 = (a + b)^2\).

Тогда получается \(p^2 - (a + b)^2\), что по формуле разности квадратов раскладывается в

\((p - a - b)(p + a + b)\).

Пояснение к пункту в):

В трёхчлене \(b^2 - c^2 - 8b + 16\) сначала выделили полный квадрат \(b^2 - 8b + 16 = (b - 4)^2\). После этого получили \((b - 4)^2 - c^2\), что есть разность квадратов. Разложение по формуле даёт \((b - 4 - c)(b - 4 + c)\), что равно \((b - c - 4)(b + c - 4)\).

Пояснение к пункту г):

В выражении \(9 - c^2 + a^2 - 6a\) сначала переписали его как

\((a^2 - 6a + 9) - c^2\).

Замечен полный квадрат

\(a^2 - 6a + 9 = (a - 3)^2\).

Тогда имеем \((a - 3)^2 - c^2\), что по формуле разности квадратов равно \((a - 3 - c)(a - 3 + c)\), то есть

\((a - c - 3)(a + c - 3)\).

а) \( (a^2 + 3b^3)^3 =a^6 + 3\,(a^2)^2 \cdot (3b^3) +3\,(a^2)\,\bigl(3b^3\bigr)^2 + (3b^3)^3=\)

\(=a^6 + 3\,a^4 \cdot 3b^3 + 3\,a^2 \cdot 9b^6 + 27\,b^9=\)

\(=a^6 + 9\,a^4b^3 + 27\,a^2b^6 + 27\,b^9= \)

\(=a^6 + 9\,a^4b^3 + 27\,a^2b^6 + 27\,b^9. \)

б) \( (1 - 2xy)^4 = 1^4 - 4 \cdot 1^3 \cdot 2xy + 6 \cdot 1^2 \cdot \bigl(2xy\bigr)^2 - 4 \cdot 1 \cdot \bigl(2xy\bigr)^3 + \bigl(2xy\bigr)^4 =\)

\(= 1 - 8xy + 6 \cdot 4x^2y^2 - 4 \cdot 8x^3y^3 + 16\,x^4y^4=\)

\(= 1 - 8\,xy + 24\,x^2y^2 - 32\,x^3y^3 + 16\,x^4y^4\)

Пояснения:

а) Формула куба двучлена:

\( (u + v)^3 = u^3 + 3u^2v + 3uv^2 + v^3. \)

В пункте (а) положили

\(u = a^2\), \(v = 3b^3\),

последовательно вычислили

\(u^3\), \(3u^2v\), \(3uv^2\) и \(v^3\).

б) При записи формулы двучлена

\(a + b\) в степени \(n\), первый член получаемого многочлена равен \(a^n\) и \(b^0\). Далее при переходе к каждому последующему члену показатель степени \(a\) уменьшается на 1, а показатель степени \(b\) увеличивается на 1, т.е. сумма показателей степеней в каждом слагаемом равна \(n\).

Для определения коэффициентов получаемого многочлена, используют треугольник Паскаля. В треугольнике Паскаля "боковые стороны" состоят из единиц, а каждое из остальных чисел равно сумме двух чисел, записанных над ним.

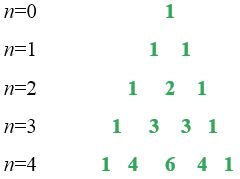
Строки треугольника Паскаля определяют коэффициенты многочлена в формуле для данной степени \(n\).

Значит, коэффициенты двучлена четвертой степени равны:

1; 4; 6; 4; 1.

Тогда формула четвёртой степени двучлена:

\( (u + v)^4 = u^4 + 4u^3v + 6u^2v^2 + 4uv^3 + v^4. \)

В пункте (б) положили

\(u = 1\), \(v = -2xy\).

При этом нужно учитывать знак при возведении \((-2xy)\) в степень:

\((-2xy)^2 = 4x^2y^2\),

\((-2xy)^3 = -8x^3y^3\),

\((-2xy)^4 = 16x^4y^4\).

При выполнении преобразований учитывали свойства степени:

\((ab)^n=a^nb^n;\)

\((a^m)^n=a^{mn}\).