Упражнение 776 - ГДЗ Алгебра 7 класс. Макарычев, Миндюк. Учебник. Страница 160
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№776 учебника 2023-2025 (стр. 160):
Из A в B одновременно выехали два мотоциклиста. Скорость одного из них в 1,5 раза больше скорости другого. Мотоциклист, который первым прибыл в B, сразу же отправился обратно. Другого мотоциклиста он встретил через 2 ч 24 мин после выезда из A. Расстояние между A и B равно 120 км. Найдите скорости мотоциклистов и расстояние от места встречи до B.
№776 учебника 2013-2022 (стр. 160):
Докажите, что:
а) сумма трёх последовательных степеней числа 2 с натуральными показателями делится на 14;
б) сумма двух последовательных степеней числа 5 с натуральными показателями делится на 30.
Подсказка
№776 учебника 2023-2025 (стр. 160):
Вспомните:
- Решение задач с помощью уравнений.
- Линейное уравнение.
- Деление и дроби.
- Свойства уравнений.
- Задачи на движение.
- Умножение десятичных дробей.
- Сложение десятичных дробей.
- Сокращение дробей.
- Единицы измерения времени.
№776 учебника 2013-2022 (стр. 160):
Вспомните:
- Степень с натуральным показателем.
- Свойства степени с натуральным показателем.
- Вынесение общего множителя за скобки.
- Свойства делимости.
Ответ
№776 учебника 2023-2025 (стр. 160):
1) \(2 \text{ч } 24 \text{ мин} =2\frac{\cancel{24}^2}{\cancel{60}^5}\text{ ч}=2\frac{2}{5}\text{ ч}=2,4\text{ ч}\)
2) \(120 \cdot 2 = 240 \text{ (км)}\) - вместе проехали первый и второй мотоциклисты.
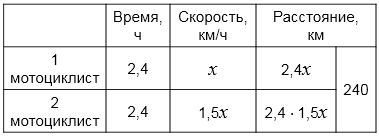
3) Составим уравнение:
а) \(2{,}4\cdot1{,}5x + 2{,}4x = 240\)
| × | 2 | 4 | |
| 1 | 5 | ||
| + | 1 | 2 | 0 |
| 2 | 4 | ||
| 3 | 6 | 0 |
\(3,6x + 2{,}4x = 240\)
\(6x = 240\)
\(x = \frac{240}{6}\)
\(x = 40 \text{ (км/ч)}\) - скорость первого мотоциклиста.
4) \(1{,}5x = 1{,}5 \cdot 40 = 60 \text{ (км/ч)}\) - скорость второго мотоциклиста.
б) \(120 - 2,4\cdot40 = 120 - 96 = \)
\(=24 \text{ (км)}\) - расстояние от места встречи до B.
Ответ: 40 км/ч, 60 км/ч, 24 км.
Пояснения:
Использованные формулы и обозначения:
\(x\) — скорость первого (медленного) мотоциклиста;
\(1{,}5x\) — скорость второго (быстрого) мотоциклиста;
\(s = vt\) — путь равен произведению скорости на время.
1. За время \(t = 2{,}4\) ч (т.е. 2 ч 24 мин) первый проехал от A до точки встречи путь
\[x \cdot 2{,}4 = 2{,}4x.\]
2. Второй за это же время прошёл путь
\[1{,}5x \cdot 2{,}4 = 3{,}6x,\]
из которых первые 120 км — от A до B, а оставшиеся — от B до места встречи, то есть получается, что вместе мотоциклисты проехали
\(120 \cdot 2 = 240 \text{ (км)}\), поэтому составляем следующее уравнение:
\(3{,}6x + 2{,}4x = 240\), откуда
\(6x = 240\) и получаем, что скорость первого мотоциклиста:
\(x = 40 \text{ (км/ч)}\).
Значит, скорость второго мотоциклиста:
\(1{,}5x = 1{,}5 \cdot 40 = 60 \text{ (км/ч)}\)
Расстояние до встречи - это расстояние, которое первый велосипедист не доехал до пункта В, тогда, учитывая то что расстояние между пунктами А и В равно 120 км, расстояние от места встречи до B равно:
\(120 - 2,4\cdot40 = 120 - 96 =\)
\(=24 \text{ (км)}\).
№776 учебника 2013-2022 (стр. 160):
а) \( 2^n\), \(2^{n+1}\), \(2^{n+2}\) - три последовательных степени числа 2 с натуральными показателями.
\( 2^n + 2^{n+1} + 2^{n+2} =\)
\(=2^n\,(1 + 2 + 2^2) = 2^n \cdot 7 =\)
\(=2\cdot7\cdot2^{\,n-1} = 14\cdot 2^{\,n-1} \) - делится на 14.
б) \( 5^n\), \( 5^{n+1} \) - две последовательные степени числа 5 с натуральными показателями.
\( 5^n + 5^{n+1} = 5^n\,(1 + 5) =\)
\(=5^n \cdot 6 = 6\cdot5\cdot5^{\,n-1} = \)
\(=30\cdot5^{\,n-1} \) - делится на 30.
Пояснения:
1. Разложение на множители: для любого числа \(a\) и натурального \(n\) верно \[ a^n + a^{n+1} = a^n(1 + a), \quad a^n + a^{n+1} + a^{n+2} = a^n(1 + a + a^2). \]
2. Свойство натуральных показателей: при \(n\ge1\) множитель \(a^n\) содержит по крайней мере один множитель \(a\), а в случае \(2^n\) — одну двойку.
3. Правило делимости произведения: если один из множителей произведения равен указанному числу, а остальные целые, то всё произведение делится на это число.
В пункте а) после разложения получаем \(14\cdot2^{n-1}\), что даёт делимость на 14.
В пункте б) получаем \(30\cdot5^{n-1}\), что даёт делимость на 30.
Вернуться к содержанию учебника