Упражнение 628 - ГДЗ Алгебра 7 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№628 учебника 2023-2025 (стр. 136):
Представьте выражение в виде одночлена:
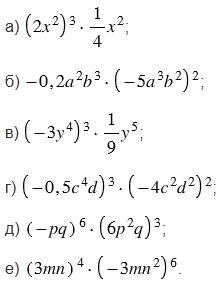
№628 учебника 2013-2022 (стр. 137):
Докажите, что выражение тождественно равно нулю:
а) \(a(b - c) + b(c - a) + c(a - b);\)
б) \(a(b + c - bc) - b(c + a - ac) + c(b - a).\)
Подсказка
№628 учебника 2023-2025 (стр. 136):
Вспомните:
- Что называют многочленом.
- Степень с натуральным показателем.
- Свойства степени с натуральным показателем.
- Умножение рациональных чисел.
- Умножение обыкновенных дробей.
- Сокращение дробей.
- Умножение десятичных дробей.
№628 учебника 2013-2022 (стр. 137):
Вспомните:
- Какие выражения называют тождеством.
- Какое выражение называют одночленом.
- Какое выражение называют многочленом.
- Умножение одночлена на многочлен.
- Приведение подобных слагаемых.
Ответ
№628 учебника 2023-2025 (стр. 136):
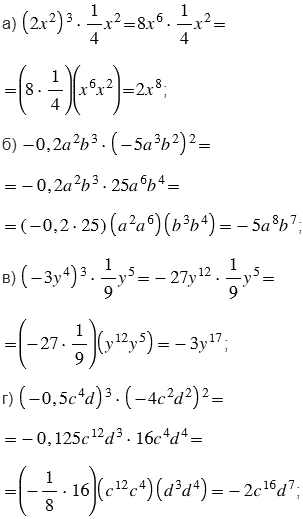
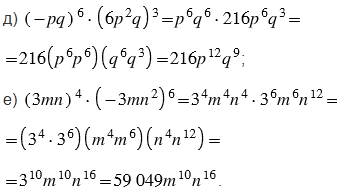
Пояснения:
При возведении отрицательного числа в степень с чётным показателем получаем положительное число, а при возведении отрицательного числа в степень с нечётным показателем получаем отрицательное число. При этом обращаем внимание на то, что на минус, стоящий перед скобками, показатель степени не влияет, на минус, стоящий в скобках, влияет только тот показатель степени, который стоит за скобками.
При возведении произведения в степень каждый множитель возводят в эту степень и полученные результаты перемножают.
При возведении степени в степень основание оставляют тем же, а показатели перемножают.
При умножении степеней с одинаковыми основаниями основание оставляют прежним, а показатели степеней складывают.
№628 учебника 2013-2022 (стр. 137):
а) \( a(b - c) + b(c - a) + c(a - b) = \)
\( = ab - ac + bc - ab + ca - bc = \)
\( = \bigl(ab - ab\bigr) + \bigl(bc - bc\bigr) + \bigl(ca - ac\bigr) = \)
\( = 0 + 0 + 0 = 0. \)
б) \( a(b + c - bc) - b(c + a - ac) + c(b - a) =\)
\( = ab + ac - abc \;-\; bc - ab + abc \;+\; bc - ca = \)
\( = \bigl(ab - ab\bigr) +\bigl(ac - ca\bigr) +\bigl(-abc + abc\bigr) +\bigl(-bc + bc\bigr) = \)
\( = 0 + 0 + 0 + 0 = 0. \)
Пояснения:
• В пункте (а) каждое слагаемое разворачивается и пары противоположных членов \(ab\) и \(-ab\), \(bc\) и \(-bc\), \(ca\) и \(-ac\) взаимно уничтожаются.
• В пункте (б) сначала умножают одночлен на многочлен, используя распределительный закон умножения. Далее приводятся подобные слагаемые и в итоге получаем 0.
• Поскольку после всех сокращений остаётся только ноль, выражения тождественно равны нулю для любых \(a\), \(b\), \(c\).
Вернуться к содержанию учебника