Упражнение 535 - ГДЗ Алгебра 7 класс. Макарычев, Миндюк. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№535 учебника 2023-2025 (стр. 124):
Не выполняя вычислений, сравните значения выражений:
а) (-0,03)8 и 0;
б) 0 и (-1,25)7;
в) (-1,75)3 и (-0,29)2;
г) 0,986 и 1,026.
№535 учебника 2013-2022 (стр. 123):
Найдите значение выражения:
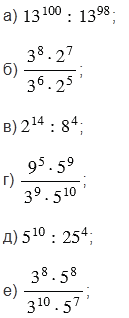
Подсказка
№535 учебника 2023-2025 (стр. 124):
Вспомните:
- Степень с натуральным показателем.
- Умножение рациональных чисел.
- Четные и нечетные числа.
- Умножение десятичных дробей.
- Сравнение рациональных чисел.
- Сравнение десятичных дробей.
№535 учебника 2013-2022 (стр. 123):
Вспомните:
- Степень с натуральным показателем.
- Свойства степени с натуральным показателем.
- Деление и дроби.
- Сокращение дробей.
- Деление десятичных дробей.
Ответ
№535 учебника 2023-2025 (стр. 124):
а) (-0,03)8 > 0;
б) 0 > (-1,25)7;
в) (-1,75)3 < (-0,29)2;
г) 0,986 < 1,026.
Пояснения:
- При возведении неотрицательного числа в степень получаем неотрицательное число.
- При возведении отрицательного числа в степень с чётным показателем получаем положительное число, а при возведении отрицательного числа в степень с нечётным показателем получаем отрицательное число.
а) (-0,03)8 > 0, так как в выражении (-0,03)8 четный показатель степени и, значит, (-0,03)8 - положительное число, которое всегда больше нуля.
б) 0 > (-1,25)7 так как в выражении (-1,25)7 нечетный показатель степени и, значит, (-1,25)7 - отрицательное число, которое всегда меньше нуля.
в) (-1,75)3 < (-0,29)2, так как в выражении (-1,75)3 нечетный показатель степени и, значит, (-1,75)3 - отрицательное число, в выражении (-0,29)2 четный показатель степени и, значит, (-0,29)2 - положительное число, а всякое отрицательное число меньше любого положительного числа.
г) 0,986 < 1,026, так как у степеней показатели степени одинаковые, при этом 0,98 < 1,02.
№535 учебника 2013-2022 (стр. 123):
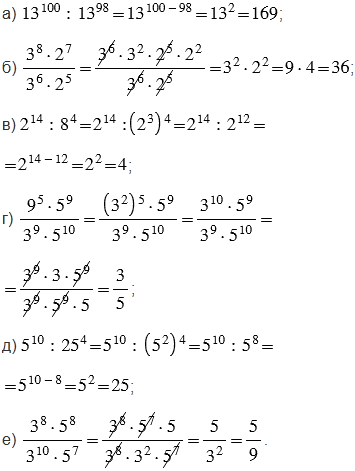
Пояснения:
Чтобы найти значения выражений, используем свойства степеней:
1) при умножении степеней с одинаковыми основаниями основание оставляют прежним, а показатели степеней складывают;
2) при делении степеней с одинаковыми основаниями основание оставляют прежним, а из показателя степени делимого вычитают показатель степени делителя;
3) чтобы возвести в степень произведение, достаточно возвести в эту степень каждый множитель и результаты перемножить;
4) при возведении степени в степень основание оставляют тем же, а показатели перемножают.
Вернуться к содержанию учебника