Задание 1.78 - ГДЗ Математика 6 класс. Виленкин, Жохов. Учебник часть 1
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№1.78 учебника 2023-2024 (стр. 24):
Найдите значение выражения:
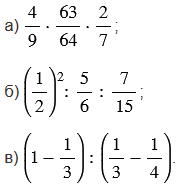
№1.78 учебника 2021-2022 (стр. 23):
Практическая работа
Оборудование: циркуль, линейка, карандаш, транспортир.
Порядок работы:
1) Проведите окружность с центром О и ее диаметр СD.
2) Используя транспортир, разделите оба развернутых угла СОD на три равных угла. Отметьте точки пересечения сторон углов с окружностью буквами С, А, В, D, М и N. Сколько получилось равных частей в круге?
3) Соедините отрезками точки С, А, В, D, М и N. Как называется этот многоугольник?
4) Сравните стороны многоугольника и радиус круга. Сделайте вывод.
Подсказка
№1.78 учебника 2023-2024 (стр. 24):
Вспомните:
- Умножение обыкновенных дробей, взаимно обратные числа.
- Деление обыкновенных дробей.
- Вычитание дробей с разными знаменателями.
- Приведение дробей к общему знаменателю.
- Основное свойство дроби (сокращение дробей).
- Вычитание дробей с одинаковыми знаменателями.
- Степень с натуральным показателем.
- Неправильные дроби.
№1.78 учебника 2021-2022 (стр. 23):
Вспомните:
- Что называют углом.
- Развернутый угол.
- Деление чисел.
- Что называют окружностью.
- Что называют отрезком.
- Что называют многоугольником.
Ответ
№1.78 учебника 2023-2024 (стр. 24):

Пояснения:
Правила, по которым выполнены вычисления:
1) произведением двух дробей является дробь, числитель которой равен произведению числителей, а знаменатель - произведению знаменателей;
2) чтобы умножить обыкновенную дробь на натуральное число, нужно ее числитель умножить на это число, а знаменатель оставить без изменения;
3) чтобы найти частное двух дробей, надо делимое умножить на число, обратное делителю. При этом помним, обратным числу 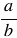 является число
является число 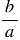 ;
;
4) чтобы возвести дробь в степень, нужно эту дробь умножить саму на себя столько раз какова степень;
5) чтобы из единицы вычесть обыкновенную дробь, нужно представить единицу в виде неправильной дроби с одинаковыми числителем и знаменателем, равными знаменателю вычитаемой дроби, а затем выполнить вычитание дробей с одинаковыми знаменателями;
6) чтобы найти сумму (разность) двух дробей с одинаковыми знаменателями, нужно сложить (вычесть) их числители, а знаменатель оставить прежним;
7) чтобы сложить (вычесть) две дроби с разными знаменателями, надо: привести данные дроби к общему знаменателю, а затем применить правило сложения (вычитания) дробей с одинаковыми знаменателями.
При выполнении умножения дробей, чтобы вычисления были проще, не надо перемножать сразу, лучше сделать это после сокращения. Сократить дробь - значит, разделить ее числитель и знаменатель на одно и то же число (наибольший общий делитель).
Также помним, дробь, у которой в знаменателе стоит единица, равна своему числителю.
№1.78 учебника 2021-2022 (стр. 23):
1800 : 3 = 600.

Многоугольник САВDМN - шестиугольник.
СА = АВ = BD = DM = MN = CN = OC.
Вывод:
Шестиугольник САВDМN - правильный, причем стороны этого шестиугольника равны радиусу окружности, на которой лежат все его вершины.
Пояснения:
1) Чертим с помощью циркуля окружность с центром О и ее диаметр СD.

2) Развернутый угол - это угол, который равен 1800, значит, СОD = 1800. Тогда, разделив, каждый из развернутых углов на три равные части, получим 6 углов по 600, так как 1800 : 3 = 600.
Чтобы разделить каждый из развернутых углов на 3 равные части, используем транспортир.
Сначала разделим верхний развернутый угол СОD на три равные части. Для этого нужно совместить центр окружности - точку О с центром транспортира так, чтобы луч ОD прошел через нулевое деление внутренней шкалы транспортира, найдем на шкале транспортира градусные меры 600 и 1200, поставим напротив них точки.

Далее чертим лучи с началом в точке О, которые пройдут через отмеченные точки и пересекут окружность в точках А и В.

Мы разделили верхний развернутый угол СОD на три равных угла АOС, АОВ и ВОD, то есть АOС = АОВ = ВОD = 600.
Затем аналогично верхнему развернутому углу СОD, делим нижний развернутый угол СОD на три равных угла СОN, МОN и DOM, то есть СОNМ = МОN = DOM = 600.

3) Соединяем отрезками точки С, А, В, D, М и N и получаем многоугольник САВDМN, который называется шестиугольником.

4) Измерив стороны шестиугольника САВDМN и радиус окружности с помощью линейки, можем сделать следующий вывод: все стороны шестиугольника равны, значит, этот шестиугольник правильный, причем стороны этого шестиугольника равны радиусу окружности, на которой лежат все его вершины.
Вернуться к содержанию учебника