Задание 461 - ГДЗ Геометрия 7-9 класс. Атанасян. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№461 учебника 2013-2022 (стр. 126):
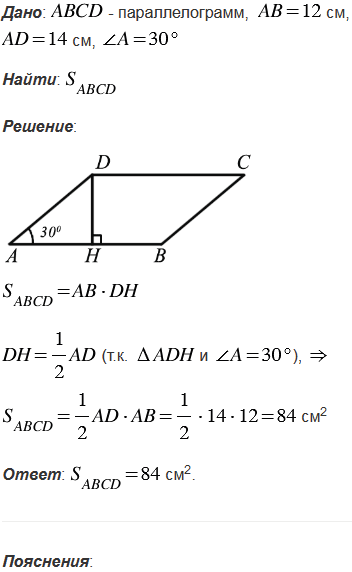
Смежные стороны параллелограмма равны 12 см и 14 см, а его острый угол равен 300. Найдите площадь параллелограмма.
№461 учебника 2023-2024 (стр. 120):
Подсказка
№461 учебника 2013-2022 (стр. 126):
Вспомните:
- Что такое параллелограмм.
- Что такое диагональ.
- Что такое площадь.
- Как найти площадь параллелограмма.
- Какой треугольник называется прямоугольным.
- Свойства прямоугольного треугольника.
№461 учебника 2023-2024 (стр. 120):
Вспомните:
- Что называют окружностью, ее элементы.
- Какой треугольник называю равнобедренным.
- Свойства равнобедренного треугольника.
- Первый признак равенства треугольников.
Ответ
№461 учебника 2013-2022 (стр. 126):

№461 учебника 2023-2024 (стр. 120):
Дано: окр.(О), её внутренняя точка A и отрезок PQ.
Построить: хорду KМ окружности, проходящую через точку А так, что АK – АМ = PQ.
Решение:
Предположим КМ искомая хорда. Отложим на ней отрезок КХ = АМ.
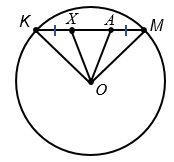
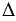 ОКМ - равнобедренный с основанием КМ, т.к. ОК = ОМ - радиусы,
ОКМ - равнобедренный с основанием КМ, т.к. ОК = ОМ - радиусы, 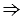
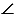 ОКМ =
ОКМ = 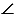 ОМК (углы при основании).
ОМК (углы при основании).
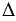 ОХК =
ОХК = 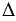 ОАМ по 1 признаку равенства треугольников (КХ = АМ по построению, ОК = ОМ - радиусы,
ОАМ по 1 признаку равенства треугольников (КХ = АМ по построению, ОК = ОМ - радиусы, 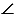 ОКМ =
ОКМ = 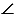 ОМК),
ОМК), 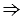 ОХ = ОА. При этом АХ = АK – КХ = АК - АМ = РQ.
ОХ = ОА. При этом АХ = АK – КХ = АК - АМ = РQ.
Построение:
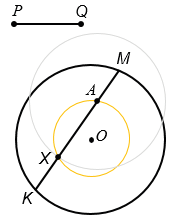
Чертим окружность с центром О радиуса ОА и окружность с центром А радиуса PQ, они пересекутся в точке Х, чертим хорду через точки А и Х она пересечет данную окружность в точках К и М. КМ - искомая хорда.
Пояснения:
Сначала решаем задачу так, как будто хорда КМ у нас уже построена. В ходе рассуждений (смотри выше решение) получаем, что нам нужно построить точку Х, которая получается пересечением двух окружностей: окружности с центром О радиуса ОА и окружности с центром А радиуса PQ. Хорда, проходящая через точки А и Х и будет искомой хордой.
Вернуться к содержанию учебника