Задание 460 - ГДЗ Геометрия 7-9 класс. Атанасян. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№460 учебника 2013-2022 (стр. 126):
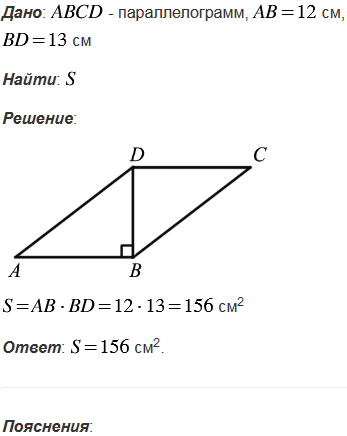
Диагональ параллелограмма, равная 13 см, перпендикулярна к стороне параллелограмма, равной 12 см. Найдите площадь параллелограмма.
№460 учебника 2023-2024 (стр. 120):
Подсказка
№460 учебника 2013-2022 (стр. 126):
Вспомните:
- Что такое параллелограмм.
- Что такое диагональ.
- Что такое площадь.
- Как найти площадь параллелограмма.
№460 учебника 2023-2024 (стр. 120):
Вспомните:
- Какой треугольник называют прямоугольным.
- Окружность, ее элементы.
- Что называют биссектрисой угла.
- Как построить биссектрису угла.
Ответ
№460 учебника 2013-2022 (стр. 126):

№460 учебника 2023-2024 (стр. 120):
Дано: 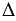 АВС - прямоугольный.
АВС - прямоугольный.
Построить: окружность с центром на одном из катетов, которая касается гипотенузы и проходит через вершину прямого угла треугольника.
Решение:
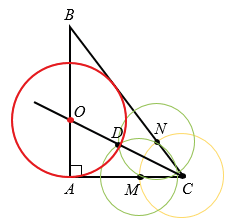
СD - биссектриса 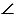 С.
С.
Окружность с центром О радиуса ОА - искомая окружность.
Пояснения:
Чертим прямоугольный треугольник АВС с прямым углом А.
Построим окружность с центром на катете АВ, которая касается гипотенузы ВС и проходит через вершину прямого угла А треугольника АВС.
Сначала построим биссектрису угла С. Для этого чертим окружность с центром в точке С произвольного радиуса, эта окружность пересечет стороны угла СА и СВ в двух точках М и N. Далее строим две окружности с центрами в точках М и N радиуса МN. Одну из точек пересечения этих окружностей внутри угла С обозначим D. Затем проводим луч СD - биссектрису угла С, который пересечет катет АВ в точке О.
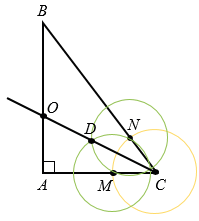
Теперь чертим окружность с центром в точке О радиуса ОА.

Окружность с центром О радиуса ОА - искомая окружность, так как она касается гипотенузы ВС и проходит через вершину прямого угла А треугольника АВС.
Вернуться к содержанию учебника