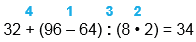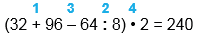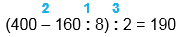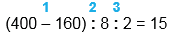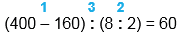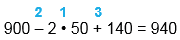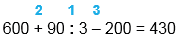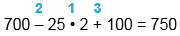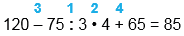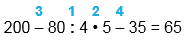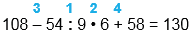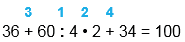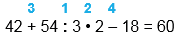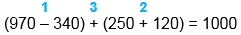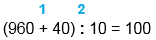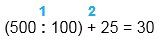Страница 18 - ГДЗ Математика 4 класс. Моро, Бантова. Учебник часть 1
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
1. 32 + (96 - 64) : 8 • 2
32 + (96 - 64) : (8 • 2)
(32 + 96 - 64 : 8) • 2
(400 - 160 : 8) : 2
(400 - 160) : 8 : 2
(400 - 160) : (8 : 2)
Подсказка
Повтори случаи табличного умножения и табличного деления, внетабличного умножения и внетабличного деления, а также правила о порядке действий и действиях со скобками.
Ответ
Решение
32 + (96 - 64) : 8 • 2 = 40
32 + (96 - 64) : (8 • 2) = 34
(32 + 96 - 64 : 8) • 2 = 240
(400 - 160 : 8) : 2 = 190
(400 - 160) : 8 : 2 = 15
(400 - 160) : (8 : 2) = 60
Пояснение
|
1) 96 - 64 = 32 2) 32 : 8 = 4 3) 4 • 2 = 8 4) 32 + 8 = 40 |
|
1) 96 - 64 = 32 2) 8 • 2 = 16 3) 32 : 16 = 2 4) 32 + 2 = 34 |
|
1) 64 : 8 = 8 2) 32 + 96 = 128 3) 128 - 8 = 120 4) 120 • 2 = 240 |
|
1) 160 : 8 = 20 2) 400 - 20 = 380 3) 380 : 2 = 190 |
|
1) 400 - 160 = 240 2) 240 : 8 = 30 3) 30 : 2 = 15 |
|
1) 400 - 160 = 240 2) 8 : 2 = 4 3) 240 : 4 = 60 |
Вопрос
2.
| 900 - 2 • 50 + 140 | |
| 600 + 90 : 3 - 200 | |
| 700 - 25 • 2 + 100 | |
| 120 - 75 : 3 • 4 + 65 | |
| 200 - 80 : 4 • 5 - 35 | |
| 108 - 54 : 9 • 6 + 58 | |
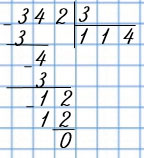
| 342 : 3 | |
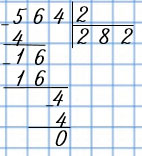
| 564 : 2 | |
| 721 : 7 |
Подсказка
Повтори случаи внетабличного умножения и деления, алгоритм письменного деления трёхзначного числа, а также правила о порядке действий.
Ответ
Решение
| 900 - 2 • 50 + 140 = 940 |
| 600 + 90 : 3 - 200 = 430 |
| 700 - 25 • 2 + 100 = 750 |
| 120 - 75 : 3 • 4 + 65 = 85 |
| 200 - 80 : 4 • 5 - 35 = 65 |
| 108 - 54 : 9 • 6 + 58 = 130 |
 |
 |
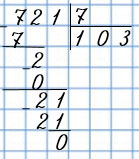 |
Пояснение
|
1) 2 • 50 = 100 2) 900 - 100 = 800 3) 800 + 140 = 940 |
|
1) 90 : 3 = 30 2) 600 + 30 = 630 3) 630 - 200 = 430 |
|
1) 25 • 2 = 50 2) 700 - 50 = 650 3) 650 + 100 = 750 |
|
1) 75 : 3 = 25 2) 25 • 4 = 100 3) 120 - 100 = 20 4) 20 + 65 = 85 |
|
1) 80 : 4 = 20 2) 20 • 5 = 100 3) 200 - 100 = 100 4) 100 - 35 = 65 |
|
1) 54 : 9 = 6 2) 6 • 6 = 36 3) 108 - 36 = 72 4) 72 + 58 = 130 |
Вопрос
3. Сравни числа.
| 796 и 800 | 312 и 320 | 1000 и 999 |
Подсказка
Повтори, как сравнивать числа.
Ответ
Вопрос
4.
| 36 + 60 : 4 • 2 + 34 |
| 42 + 54 : 3 • 2 - 18 |
| (760 + 100) - (430 + 230) |
| (970 - 340) + (250 + 120) |
Подсказка
Ответ
Решение
| 36 + 60 : 4 • 2 + 34 = 100 |
| 42 + 54 : 3 • 2 - 18 = 60 |
| (760 + 100) - (430 + 230) = 200 |
| (970 - 340) + (250 + 120) = 1000 |
Пояснение
|
1) 60 : 4 = 15 2) 15 • 2 = 30 3) 36 + 30 = 66 4) 66 + 34 = 100 |
|
1) 54 : 3 = 18 2) 18 • 2 = 36 3) 42 + 36 = 78 4) 78 - 18 = 60 |
|
1) 760 + 100 = 860 2) 430 + 230 = 660 3) 860 - 660 = 200 |
|
1) 970 - 340 = 630 2) 250 + 120 = 370 3) 630 + 370 = 1000 |
Вопрос
5. Вычисли и проверь деление умножением.
| 624 : 6 | 135 : 3 |
| 963 : 3 | 825 : 5 |
| 482 : 2 | 248 : 8 |
| 147 : 7 | 616 : 2 |
| 728 : 7 | 453 : 3 |
Ответ
Решение
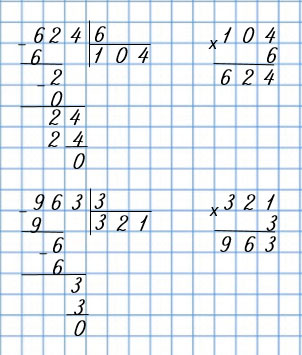 |
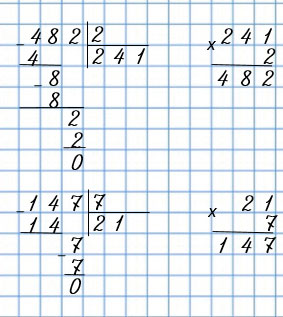 |
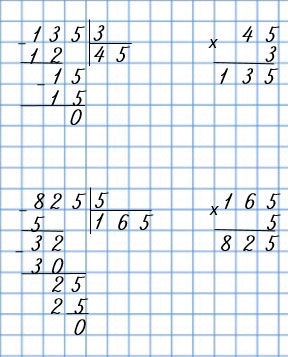 |
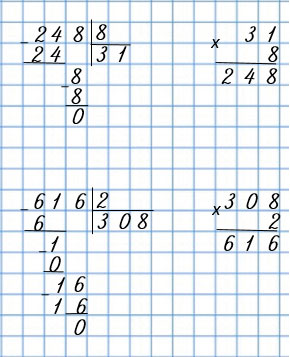 |
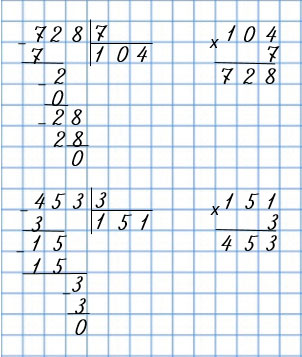 |
Пояснение
Чтобы проверить деление умножением, нужно частное умножить на делитель и в результате умножения должно получится делимое.
Пишу: 482 : 2.
Делю сотни: сотен 4.
Разделю 4 на 2. В частном будет 2 сот.
Умножу: 2 • 2 = 4. Разделили 4 сот.
Вычту: 4 - 4 = 0. Сотни разделили все.
Делю десятки: десятков 8.
Разделю 8 на 2. В частном будет 4 дес.
Умножу: 4 • 2 = 8. Разделили 8 дес.
Вычту: 8 - 8 = 0. Десятки разделили все.
Делю единицы: единиц 2.
Разделю 2 на 2. В частном будет 1 ед.
Умножу: 1 • 2 = 2. Разделили 2 ед.
Вычту: 2 - 2 = 0. Единицы разделили все.
Читаю ответ: 241.
Пишу: 241 • 2.
Умножаю единицы: 1 • 2 = 2. Пишу 2 под единицами.
Умножаю десятки: 4 • 2 = 8. Пишу 8 под десятками.
Умножаю сотни: 2 • 2 = 4. Пишу 4 под сотнями.
Читаю ответ: 482.
Далее рассуждаю аналогично.
Вопрос
6.
| 346 + 458 | 503 + 204 |
| 157 + 484 | 308 + 106 |
| 832 - 456 | 603 - 28 |
| 621 - 241 | 204 - 39 |
Ответ
Решение

Пояснение
Пишу (единицы под единицами, десятки под десятками, сотни под сотнями): 346 + 458.
Складываю единицы: 6 + 8 = 14
14 ед. - это 1 дес. 4 ед.; 4 ед. пишу под единицами, а 1 дес. запомню и прибавлю к десяткам.
Складываю десятки: 4 + 5 = 9, да ещё 1.
9 + 1 = 10.
10 дес. - это 1 сот. 0 дес.; 0 дес. пишу под десятками, а 1 сот. запомню и прибавлю к сотням.
Складываю сотни: 3 + 4 = 7, да ещё 1.
7 + 1 = 8.
Пишу под сотнями 8.
Читаю ответ: 804.
Пишу (единицы под единицами, десятки под десятками, сотни под сотнями): 621 - 241.
Вычитаю единицы: 1 - 1 = 0. Пишу 0 под единицами.
Вычитаю десятки. Из 2 дес. нельзя вычесть 4 дес. Беру 1 сот. (Чтобы не забыть об этом, ставлю точку над цифрой 6.) 1 сот. и 2 ед. - это 12 дес. Из 12 дес. вычитаю 4, получится 8. Пишу под десятками 8.
Вычитаю сотни. Было 6 сот., но 1 сот. взяли при вычитании десятков. Осталось 5 сот.
5 - 2 = 3. Пишу под сотнями 3.
Читаю ответ: 380.
Далее рассуждаю аналогично.
Вопрос
7.
| 318 • 3 | 824 : 4 |
| 247 • 4 | 565 : 5 |
| 207 • 4 | 234 : 9 |
| 108 • 6 | 632 : 8 |
| 434 : 7 | 984 : 8 |
Ответ
Решение
 |
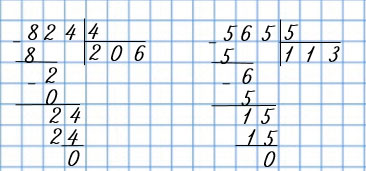 |
 |
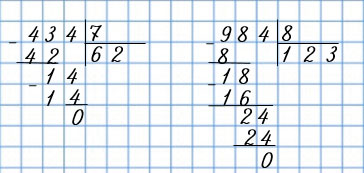 |
Пояснение
Пишу: 565 : 5.
Делю сотни: сотен 5.
Разделю 5 на 5. В частном будет 1 сот.
Умножу: 1 • 5 = 5. Разделили 5 сот.
Вычту: 5 - 5 = 0. Сотни разделили все.
Делю десятки: десятков 6.
Разделю 6 на 5. В частном будет 1 дес.
Умножу: 1 • 5 = 5. Разделили 5 дес.
Вычту: 6 - 5 = 1. Осталось разделить 1 дес.
Делю единицы: 1 дес. и 5 ед. - это 15 ед.
Разделю 15 на 5. В частном будет 3 ед.
Умножу: 3 • 5 = 15. Разделили 15 ед.
Вычту: 15 - 15 = 0. Единицы разделили все.
Читаю ответ: 113.
Если при делении сразу сносим два числа, то в частном нужно записать 0.
Пишу: 318 • 3.
Умножаю единицы: 8 • 3 = 24. 24 ед. - это 1 дес. 4 ед, 4 ед. пишу под единицами, а 2 дес. запомню и прибавлю к десяткам после умножения десятков.
Умножаю десятки: 1 • 3 = 3. К 3 дес. прибавляю 2 дес., который получен при умножении единиц: 3 + 2 = 5. Пишу 5 под десятками.
Умножаю сотни: 3 • 3 = 9. Пишу 9 под сотнями.
Читаю ответ: 954.
Далее рассуждаю аналогично.
Вопрос
8. Запиши выражения и найди их значения.
1) Сумму чисел 960 и 40 уменьшить в 10 раз.
2) Частное чисел 500 и 100 увеличить на 25.
Ответ
Вопрос
9. На поездку в магазин и обратно мальчик затратил 1 ч 10 мин. Туда он ехал на велосипеде 25 мин, в магазине пробыл 15 мин. Сколько минут мальчик ехал обратно?
Подсказка
Ответ
Решение
1) 25 + 15 = 40 (мин) - на дорогу туда и время в магазине.
2) 1 ч 10 мин = 70 мин
70 - 40 = 30 (мин)
Ответ: 30 мин ехал обратно.
Пояснение
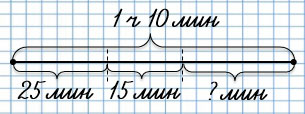
Сколько времени потратил мальчик в магазине и на дорогу до магазина?
1) 25 + 15 = 40 (мин)
Сколько минут мальчик ехал обратно?
2) 70 - 40 = 30 (мин)
Сначала узнаем, сколько времени потратил мальчик до магазина и в магазине:
1) 25 + 15 = 40 (мин)
Мы знаем, что общее затраченное время - 1 ч 10 мин.
1 ч 10 мин = 70 мин
Узнаем, сколько времени мальчик ехал обратно. Для этого из всего времени вычтем время, которое мальчик потратил до магазина и в магазине:
2) 70 - 40 = 30 (мин)
Вопрос
10. Из 28 м ткани сшили 7 одинаковых платьев. Сколько потребуется ткани, чтобы сшить 12 таких платьев? Сколько таких платьев можно сшить из 60 м ткани?
Подсказка
Ответ
Решение
1) 28 : 7 = 4 (м) - на 1 платье.
2) 4 • 12 = 48 (м) - на 12 платьев.
3) 60 : 4 = 15 (пл.) - можно сшить из 60 м.
Ответ: 48 м, 15 платьев.
Пояснение

Сколько метров ткани расходуется на 1 платье?
1) 28 : 7 = 4 (м)
Сколько потребуется ткани, чтобы сшить 12 таких платьев?
2) 4 • 12 = 48 (м)
Сколько таких платьев можно сшить из 60 м ткани?
3) 60 : 4 = 15 (пл.)
Мы знаем, что на 7 одинаковых платьев ушло 28 м ткани. Узнаем, сколько метров ткани расходуется на 1 платье:
1) 28 : 7 = 4 (м)
На 1 платье нужно 4 м ткани, нам нужно 12 таких платьев:
2) 4 • 12 = 48 (м)
На 1 платье требуется 4 м ткани, у нас есть 60 м ткани. Узнаем, сколько платьев получится из этого количества материала:
3) 60 : 4 = 15 (пл.)
Вопрос
Выберите год учебника
Стр. 18 учебника 2023-2025:
11. 1) Выпиши названия всех многоугольников.
2) Найди периметр и площадь квадрата ABCD.
3) Что можно сказать о площадях прямоугольника AMKD и треугольника ABC? Подтверди свой ответ.

Стр. 18 учебника 2011-2022:
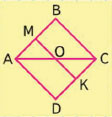
11. 1) Выпиши названия всех многоугольников.
2) Найди периметр и площадь квадрата ABCD.
3) Сравни площадь прямоугольника AMKD и площадь треугольника ABC.
Подсказка
Повтори, что такое многоугольник и как найти его периметр и площадь.
Ответ
Решение
1) AMO, OCK, ABC, ACD, OMBC, OADK, AMKD, MBCK, ABCD, ABCKO, AMOCD, ABCOKD, OMBCDA.
2) 2 • 4 = 8 (см) - периметр ABCD.
2 • 2 = 4 (см2) - площадь ABCD.
3) SAMKD = SABC.
Пояснение
2) Измерим стороны ABCD:
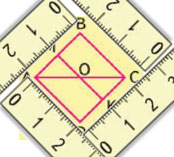
AB = BC = CD = AD = 2 см
Периметр квадрата равен произведению длины любой его стороны на четыре (так как всего его стороны равны) или сумме длин всех его сторон:
2 • 4 = 8 (см)
ИЛИ
2 + 2 + 2 + 2 = 8 (см)
Площадь квадрата можно определить, умножив сторону саму на себя:
2 • 2 = 4 (см2)
3) 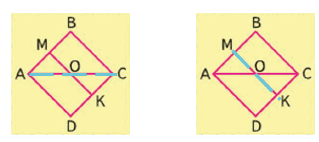
Если мы начертим такой же квадрат, вырежем его и перегнём по отрезку АС, то увидим, что ABC = ADC, значит площадь каждого из этих треугольников равна половине площади квадрата ABCD.
Аналогично перегнём квадрат по отрезку МК. Видим, что AMKD = MBCK. Значит, площадь каждого из этих прямоугольников равна половине прямоугольника AMKD.
Делаем вывод:
Прямоугольник AMKD − это половина квадрата ABCD;
Треугольник ABC − тоже половина квадрата ABCD;
Значит, SAMKD=SABC.
Вопрос
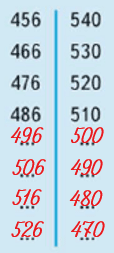
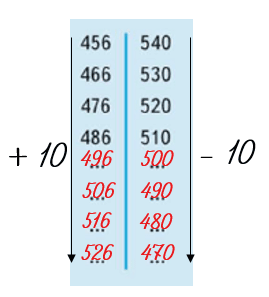
Продолжи ряды чисел.

Подсказка
Повтори, что значит увеличить/уменьшить на ... чисел.
Ответ
Вернуться к содержанию учебника