Номер 2 - ГДЗ Алгебра 8 класс. Мерзляк, Полонский. Учебник. Страница 210
Вернуться к содержанию учебника
Упражнения §24. Когда сделаны уроки. Страница 210
Вопрос
Даны два высказывания:
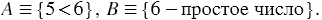
Определите, истинным или ложным является высказывание:
Подсказка
Вспомните:
- Что называют высказыванием.
- Логические операции.
Ответ
1) Ложно; 2) Истинно; 3) Ложно;
4) Ложно; 5) Ложно; 6) Истинно.
Пояснения:
Математическая логика - наука, которая изучает математические доказательства (логически безупречные рассуждения). Она учит, как надо рассуждать, чтобы получить верные выводы. Высказывание - это любое утверждение, относительно которого имеет смысл говорить, что оно истинно или ложно. Высказывания обозначают прописными буквами латинского алфавита: A, B, C и т.д.
Нам даны в задании два высказывания:
А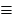 {5<6}, которое является истинным;
{5<6}, которое является истинным;
В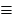 {6 - простое число}, которое является ложным.
{6 - простое число}, которое является ложным.
1) Так как высказывание В ложно, то и высказывание А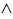 В ложно.
В ложно.
Конъюнкцией (или логическим произведением) двух высказываний А и В называют высказывание, которое истинно, если каждое из высказываний А и В истинно, и ложно, если хотя бы одно из них ложно. Конъюнкцию высказываний А и В обозначают так: А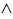 В (читают "А и В" или "А конъюнкция В").
В (читают "А и В" или "А конъюнкция В").
2) Так как высказывание А истинно, то высказывание А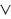 В также истинно.
В также истинно.
Дизъюнкцией (или логической суммой) двух высказываний А и В называют высказывание, которое истинно, если хотя бы одно из высказываний А или В истинно, и ложно, если они оба ложны. Дизъюнкцию высказываний А и В обозначают так: А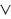 В (читают "А или В" или "А дизъюнкция В").
В (читают "А или В" или "А дизъюнкция В").
3) Так как высказывание В ложно, то и высказывание А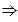 В ложно.
В ложно.
Импликацией (или логическим следованием) двух высказываний А и В называют такое высказывание А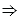 В (читают: "если А, то В"), которое ложно при условии, что высказывание А истинно, а высказывание В ложно, а во всех остальных случаях оно истинно.
В (читают: "если А, то В"), которое ложно при условии, что высказывание А истинно, а высказывание В ложно, а во всех остальных случаях оно истинно.
4) Высказывание А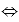 В ложно, так как если А
В ложно, так как если А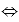 В является истинным высказыванием, то А = В, а это не так.
В является истинным высказыванием, то А = В, а это не так.
Высказывания А и В называют логически эквивалентными, если они или оба истинны, или оба ложны.
5) Данное высказывание можно прочесть как "не А", то есть так как высказывание А истинно, то данное высказывание ложно.
6) Данное высказывание можно прочесть как "не В", то есть так как высказывание В ложно, то данное высказывание истинно.
Вернуться к содержанию учебника