Применение подобия фигур к доказательству теорем и решению задач
Доказательство теорем
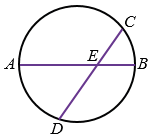
Рис. 1
Теорема
| Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды. |
Дано: окружность, АВ и СD - хорды, АВ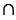 СD = Е (рис. 2).
СD = Е (рис. 2).
Доказать: АЕ ВЕ = СЕ
ВЕ = СЕ DЕ.
DЕ.
Доказательство:
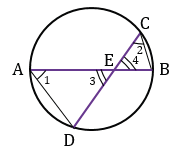
Рис. 2
В 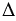 АDЕ и
АDЕ и 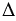 СВЕ:
СВЕ: 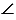 1 =
1 = 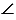 2, т.к. они вписанные и опираются на одну и ту же дугу ВD (смотри следствие 1 из теоремы о вписанном угле),
2, т.к. они вписанные и опираются на одну и ту же дугу ВD (смотри следствие 1 из теоремы о вписанном угле), 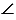 3 =
3 = 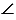 4 как вертикальные углы, следовательно, треугольники АDЕ и СВЕ подобны (по 1 признаку подобия треугольников). В подобных треугольниках сходственные стороны пропорциональны, поэтому
4 как вертикальные углы, следовательно, треугольники АDЕ и СВЕ подобны (по 1 признаку подобия треугольников). В подобных треугольниках сходственные стороны пропорциональны, поэтому 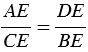 , откуда АЕ
, откуда АЕ ВЕ = СЕ
ВЕ = СЕ DЕ.
DЕ.
Теорема доказана.
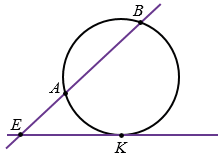
Рис. 3
Теорема
|
Если через внешнюю точку к окружности проведены касательная и секущая, то квадрат отрезка касательной равен произведению отрезков секущей.
|
Дано: окружность, ЕК - касательная, К - точка касания, АВ - секущая, АВ ЕК = Е (рис. 4).
ЕК = Е (рис. 4).
Доказать: ЕК2 = ЕА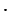 ЕВ.
ЕВ.
Доказательство:
Рис. 4
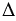 ЕKA и
ЕKA и 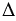 ЕBK:
ЕBK: 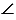 1 =
1 = 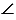 2 , т.к. каждый из них измеряется половиной дуги АK (
2 , т.к. каждый из них измеряется половиной дуги АK (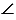 1 — вписанный в окружность и опирающийся на дугу АK, а
1 — вписанный в окружность и опирающийся на дугу АK, а 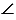 2 — угол между касательной к окружности и хордой),
2 — угол между касательной к окружности и хордой), 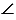 3 — общий угол этих треугольников, значит, по 1 признаку подобия треугольников
3 — общий угол этих треугольников, значит, по 1 признаку подобия треугольников 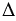 EKA
EKA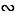
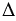 EBK. Отсюда следует, что
EBK. Отсюда следует, что 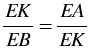 или EK2 = EA
или EK2 = EA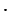 EВ.
EВ.Теорема
|
Если через точку Е, лежащую вне окружности, проведены две секущие, то произведение отрезков одной секущей равно произведению отрезков другой секущей (рис. 5).
|
Дано: А1В1 и А2В2 - секущие, А1В1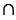 А2В2 = Е.
А2В2 = Е.
Доказать: ЕА1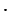 ЕВ1 = ЕА2
ЕВ1 = ЕА2 ЕВ2.
ЕВ2.
Доказательство:
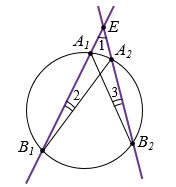
Рис. 5
В  ЕВ1А2 и
ЕВ1А2 и  ЕВ2А1:
ЕВ2А1: 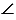 1 - общий,
1 - общий, 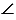 2 =
2 = 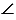 3, т.к. каждый из них измеряется половиной дуги А1А2 (вписанные углы), значит, по 1 признаку подобия треугольников
3, т.к. каждый из них измеряется половиной дуги А1А2 (вписанные углы), значит, по 1 признаку подобия треугольников 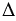 ЕВ1А2
ЕВ1А2
 ЕВ2А1. Отсюда следует, что
ЕВ2А1. Отсюда следует, что 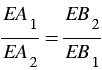 или ЕА1
или ЕА1 ЕВ1 = ЕА2
ЕВ1 = ЕА2 ЕВ2.
ЕВ2.
Теорема доказана.
Решение задач
Задача 1
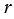 , один конец которых совпадает с данной точкой А этой окружности, есть окружность, построенная на отрезке АС как на диаметре (рис. 6).
, один конец которых совпадает с данной точкой А этой окружности, есть окружность, построенная на отрезке АС как на диаметре (рис. 6).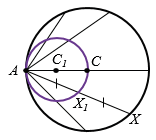
Рис. 6
Решение:
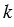 =
= 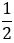 любая точка Х окружности с центром С и радиусом
любая точка Х окружности с центром С и радиусом 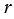 перейдёт в точку Х1 — середину хорды АХ. По 30 свойству гомотетии при указанной гомотетии окружность с центром С и радиусом
перейдёт в точку Х1 — середину хорды АХ. По 30 свойству гомотетии при указанной гомотетии окружность с центром С и радиусом 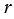 переходит в окружность с центром С1 в середине отрезка АС и радиусом
переходит в окружность с центром С1 в середине отрезка АС и радиусом 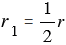 . Эта окружность и является искомым множеством точек.
. Эта окружность и является искомым множеством точек.Задача 2
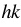 и точка А внутренней области этого угла. Постройте окружность, проходящую через точку А и касающуюся сторон угла.
и точка А внутренней области этого угла. Постройте окружность, проходящую через точку А и касающуюся сторон угла.Решение:
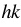 , А — данная точка (рис. 7).
, А — данная точка (рис. 7).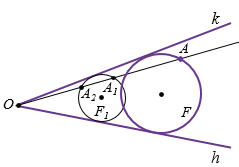
Рис. 7
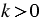 окружность F перейдёт в окружность F1, которая, очевидно, будет касаться сторон угла
окружность F перейдёт в окружность F1, которая, очевидно, будет касаться сторон угла 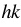 . Точка А перейдёт в одну из точек пересечения луча ОА с окружностью F1: А1 или А2 (на рисунке 7, точка А переходит в точку А1). Ясно, что при гомотетии с центром в точке О и коэффициентом
. Точка А перейдёт в одну из точек пересечения луча ОА с окружностью F1: А1 или А2 (на рисунке 7, точка А переходит в точку А1). Ясно, что при гомотетии с центром в точке О и коэффициентом 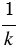 окружность F1 перейдёт в окружность F. Отсюда вытекает следующий способ решения задачи.
окружность F1 перейдёт в окружность F. Отсюда вытекает следующий способ решения задачи.Строим произвольную окружность F1, касающуюся сторон угла 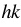 , и находим точки А1 и А2 пересечения луча ОА с этой окружностью. Далее строим окружность F, в которую переходит окружность F1 при гомотетии с центром в точке О, переводящей одну из точек А1 или А2 в точку А (см. задачу 1323). Окружность F – искомая. Построение выполнено на рисунке 8. На этом рисунке
, и находим точки А1 и А2 пересечения луча ОА с этой окружностью. Далее строим окружность F, в которую переходит окружность F1 при гомотетии с центром в точке О, переводящей одну из точек А1 или А2 в точку А (см. задачу 1323). Окружность F – искомая. Построение выполнено на рисунке 8. На этом рисунке 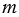 — биссектриса угла
— биссектриса угла 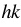 , C1 — произвольная её точка, C1H1
, C1 — произвольная её точка, C1H1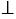
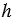 и AC
и AC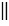 А1C1.
А1C1.
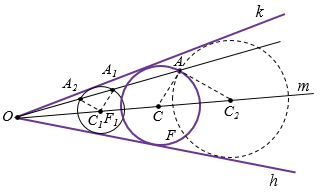
Рис. 8
Задача всегда имеет два решения, так как можно рассматривать две гомотетии: одну, при которой точка А1 переходит в точку А, другую — при которой точка А2 переходит в точку А. На рисунке 8 второе решение изображено штриховой линией.
Советуем посмотреть:
Теоремы о периметрах и площадях подобных фигур
Правило встречается в следующих упражнениях:
7 класс
Задание 1328, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1330, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1332, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1333, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1360, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1365, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 17, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 18, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 19, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 20, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник