Гомотетия. Свойства гомотетии
На плоскости отметим точку О и возьмем любое число 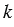 , отличное от нуля. Каждой точке Е плоскости, отличной от точки О, поставим в соответствие точку Е1 по следующему правилу:
, отличное от нуля. Каждой точке Е плоскости, отличной от точки О, поставим в соответствие точку Е1 по следующему правилу:
1) точка Е1 лежит на луче ОЕ, если 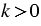 (рис. 1,
(рис. 1, 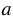 ), и точка Е1 лежит на продолжении луча ОЕ, если
), и точка Е1 лежит на продолжении луча ОЕ, если 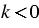 (рис. 1, б);
(рис. 1, б);
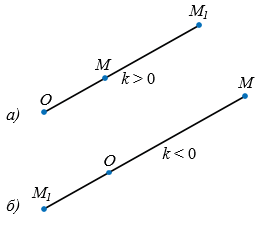
Рис. 1
2) ОМ1 = 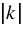 ОМ.
ОМ.
Точка О соответствует сама себе.
Обратите внимание, указанное правило можно коротко записать с помощью векторов в следующем виде: 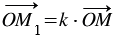 , т.к. произведением ненулевого вектора
, т.к. произведением ненулевого вектора 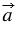 на число
на число 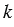 называется такой вектор
называется такой вектор 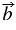 , длина которого равна
, длина которого равна 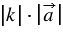 , причём векторы
, причём векторы 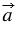 и
и 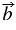 сонаправлены при
сонаправлены при 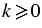 и противоположно направлены при
и противоположно направлены при 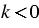 .
.
При заданном соответствии каждая точка плоскости оказывается сопоставленной некоторой единственной точке.
Рассматриваемое соответствие определяет преобразование плоскости, которое называется гомотетией или центральным подобием. Число 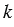 называется коэффициентом гомотетии, а точка О - центром гомотетии. Центр гомотетии является неподвижной точкой.
называется коэффициентом гомотетии, а точка О - центром гомотетии. Центр гомотетии является неподвижной точкой.
Соответственные при гомотетии фигуры F1 и F называют гомотетичными.
На рисунке 2, 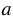 , б изображены гомотетичные фигуры F1 и F с центром гомотетии в точке О и коэффициентом
, б изображены гомотетичные фигуры F1 и F с центром гомотетии в точке О и коэффициентом 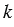 = 3.
= 3.
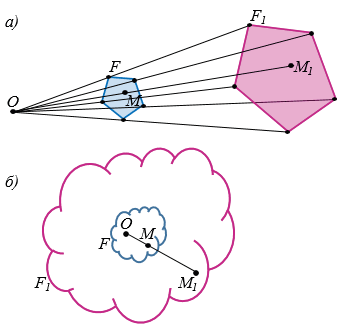
Рис. 2
На рисунке 3, 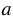 , б изображены гомотетичные фигуры F1 и F с центром гомотетии в точке О и коэффициентом
, б изображены гомотетичные фигуры F1 и F с центром гомотетии в точке О и коэффициентом 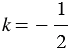 .
.
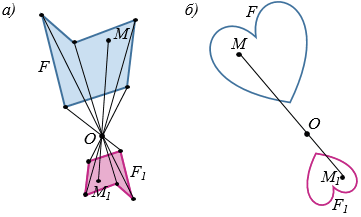
Рис. 3
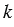 = –1, то каждая точка фигуры F переходит в симметричную ей точку относительно центра О, поэтому фигура F1 получается центральной симметрией из фигуры F (рис. 4). Другими словами, центральная симметрия является частным случаем гомотетии (когда коэффициент гомотетии равен –1).
= –1, то каждая точка фигуры F переходит в симметричную ей точку относительно центра О, поэтому фигура F1 получается центральной симметрией из фигуры F (рис. 4). Другими словами, центральная симметрия является частным случаем гомотетии (когда коэффициент гомотетии равен –1).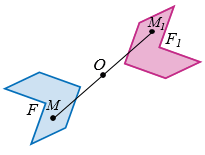
Рис. 4
Свойства гомотетии
10. При гомотетии с коэффициентом, отличным от единицы, прямая, проходящая через центр гомотетии, переходит в себя, а прямая, не проходящая через центр гомотетии, — в параллельную ей прямую (рис.5, 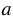 , б).
, б).
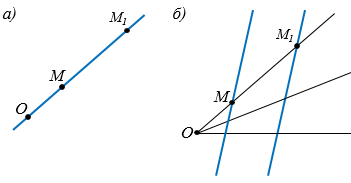
Рис. 5
20. Если при гомотетии с коэффициентом 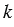 концы отрезка АВ переходят в точки А1 и В1, то отрезок АВ переходит в отрезок А1В1, причём А1В1 =
концы отрезка АВ переходят в точки А1 и В1, то отрезок АВ переходит в отрезок А1В1, причём А1В1 = 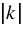 AB (рис. 6).
AB (рис. 6).
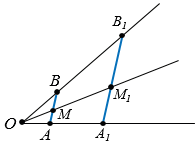
Рис. 6
30. При гомотетии с коэффициентом 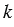 окружность с центром С и радиусом
окружность с центром С и радиусом 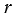 переходит в окружность с центром С1 и радиусом
переходит в окружность с центром С1 и радиусом 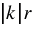 , где С1 — точка, в которую переходит точка С.
, где С1 — точка, в которую переходит точка С.
Теорема
|
При гомотетии с коэффициентом
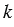 многоугольник переходит в подобный ему многоугольник, причём коэффициент подобия многоугольников равен многоугольник переходит в подобный ему многоугольник, причём коэффициент подобия многоугольников равен 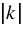 . . |
Доказательство:
Рассмотрим произвольный многоугольник А1А2...Аn. Из свойства 20 следует то, что при гомотетии с коэффициентом 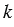 многоугольник А1А2...Аn переходит в многоугольник В1В2...Вn, при этом В1В2 =
многоугольник А1А2...Аn переходит в многоугольник В1В2...Вn, при этом В1В2 = 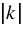 А1А2, В2В3 =
А1А2, В2В3 = 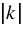 А2А3, ..., ВnВ1 =
А2А3, ..., ВnВ1 = 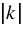 АnА1 (рис. 7 для случая, когда
АnА1 (рис. 7 для случая, когда 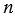 = 5).
= 5).
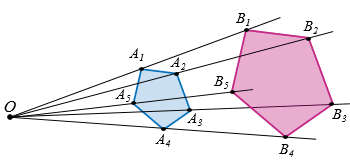
Рис. 7
При гомотетии угол переходит в равный ему угол, тогда 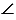 А1 =
А1 = 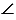 В1,
В1, 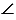 А2 =
А2 = 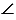 В2, ...,
В2, ..., 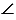 Аn =
Аn = 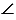 Вn.
Вn.
Из полученных равенств можно сделать вывод о том, что В1В2...Вn 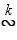 А1А2...Аn.
А1А2...Аn.
Теорема доказана.
Советуем посмотреть:
Теоремы о периметрах и площадях подобных фигур
Применение подобия фигур к доказательству теорем и решению задач
Правило встречается в следующих упражнениях:
7 класс
Задание 1313, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1322, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1334, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1351, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1357, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1366, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1427, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 10, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 11, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 16, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник