Теоремы о периметрах и площадях подобных фигур

Теорема о периметрах подобных фигур

Периметр многоугольника - это сумма длин всех его сторон.

Теорема

Доказательство:

Пусть многоугольники А₁А₂...А_n и В₁В₂...В_n с коэффициентом 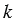. Тогда А₁А₂ = 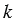В₁В₂, А₂А₃ = 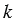В₂В₃, ..., А_nА₁ = 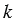В_nВ₁.

Найдем отношение периметров многоугольников А₁А₂...А_n и В₁В₂...В_n, используя полученные равенства:

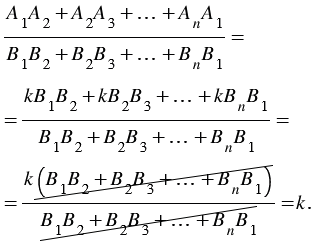
Теорема доказана.

Теорема о площадях подобных фигур

Теорема

Доказательство:

Ход рассуждений не зависит от числа сторон этих многоугольников, поэтому рассмотрим для определенности случай, когда 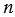= 5.

Пусть многоугольники А₁А₂А₃А₄А₅ и В₁В₂В₃В₄В₅ с коэффициентом 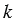. Тогда А₁А₂ = 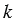В₁В₂, А₂А₃ = 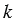В₂В₃, А₃А₄ = 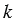В₃В₄, А₄А₅ = 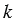В₄В₅, А₅А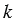₁ = В₅В₁.

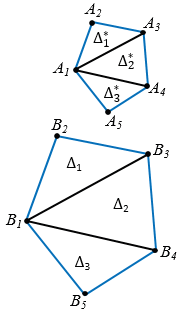
Разобьем многоугольник А₁А₂А₃А₄А₅ на треугольники 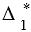, , 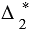, 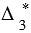а многоугольник В₁В₂В₃В₄В₅ на треугольники , , .

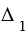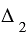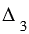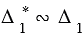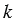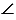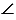По второму признаку подобия треугольников: с коэффициентом подобия , так как А₁ = В₁, .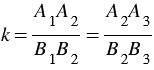

Также по второму признаку подобия треугольников: 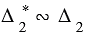с коэффициентом подобия 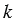, так как 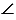А₁А₃А₄ = 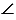В₁В₃В₄ (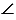А₃ = 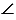В₃ по условию и 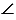А₁А₃А₂ = 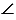В₁В₃В₂ из подобия 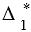и ), .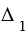

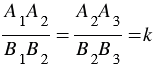Аналогично доказывается, что .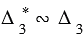

По теореме о площадях подобных треугольников:

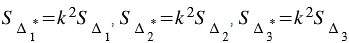
Сложим эти три равенства, получим:

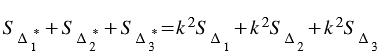или в правой части полученного равенства можно вынести 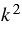за скобки, тогда .

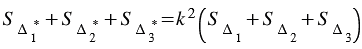Откуда, учитывая свойство площадей, получим:

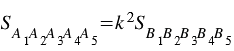или .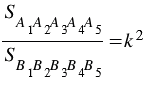

Теорема доказана.