Подобные многоугольники
При дальнейших рассуждениях мы будем говорить о многоугольниках, и под термином "многоугольник" будем понимать только выпуклый многоугольник.
Одноимённые многоугольники - это многоугольники, которые имеют одинаковое число углов, а, значит, и сторон.
Пусть А1А2...Аn и В1В2...Вn - два одноименных выпуклых многоугольника, причем углы одного многоугольника соответственно равны углам другого: 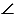 В1 =
В1 = 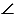 А1,
А1, 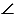 В2 =
В2 = 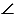 А2, ...,
А2, ..., 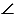 Вn =
Вn = 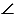 An. В данном случае стороны В1В1 и А1А2, В2В3 и А2А3 и т.д. называют сходственными сторонами. На рисунке 1 изображены два четырехугольника А1А2А3А4 и В1В2В3В4, причем
An. В данном случае стороны В1В1 и А1А2, В2В3 и А2А3 и т.д. называют сходственными сторонами. На рисунке 1 изображены два четырехугольника А1А2А3А4 и В1В2В3В4, причем 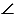 В1 =
В1 = 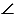 А1,
А1, 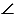 В2 =
В2 = 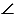 А2,
А2, 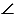 В3 =
В3 = 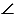 А3,
А3, 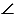 В4 =
В4 = 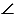 A4. Сходственными являются стороны В1В1 и А1А2, В2В3 и А2А3, В3В4 и А3А4, В4В1 и А4А1.
A4. Сходственными являются стороны В1В1 и А1А2, В2В3 и А2А3, В3В4 и А3А4, В4В1 и А4А1.
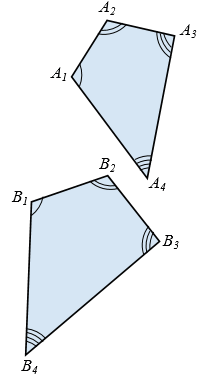
Рис. 1
Нам известно, что отношением отрезков АВ и А1В1 называется отношение их длин, т.е. 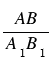 . Отрезки А1В1 и С1D1 пропорциональны отрезкам АВ и СD, если
. Отрезки А1В1 и С1D1 пропорциональны отрезкам АВ и СD, если 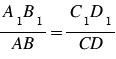 . При этом, если
. При этом, если 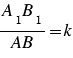 , то будем писать
, то будем писать 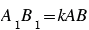 .
.
|
Многоугольник F1 называется подобным одноимённому многоугольнику F, если углы многоугольника F1 соответственно равны углам многоугольника F, а их сходственные стороны пропорциональны.
|
Число 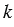 , равное отношению сходственных сторон многоугольников F1 и F, называется коэффициентом подобия многоугольника F1 относительно многоугольника F или, коротко, коэффициентом подобия многоугольников F1 и F. При этом
, равное отношению сходственных сторон многоугольников F1 и F, называется коэффициентом подобия многоугольника F1 относительно многоугольника F или, коротко, коэффициентом подобия многоугольников F1 и F. При этом 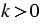 , так как отношение длин отрезков — положительное число.
, так как отношение длин отрезков — положительное число.
Если многоугольник F1 подобен многоугольнику F, то пишут: F1 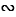 F или F1
F или F1 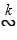 F, где
F, где 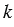 - коэффициент подобия F1 относительно F. Ясно, что если F1
- коэффициент подобия F1 относительно F. Ясно, что если F1 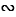 F с коэффициентом
F с коэффициентом 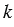 , то F
, то F 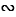 F1 с коэффициентом
F1 с коэффициентом 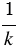 (так как коэффициент подобия показывает во сколько раз стороны одного многоугольника больше или меньше сторон другого).
(так как коэффициент подобия показывает во сколько раз стороны одного многоугольника больше или меньше сторон другого).
На рисунке 1 В1В2В3В4 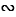 А1А2А3А4, где
А1А2А3А4, где 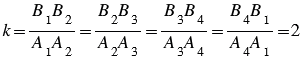 .
.
Подобие треугольников является частным случаем подобия многоугольников.
Если два многоугольника равны, то их углы соответственно равны и сходственные стороны равны. Значит, два равных многоугольника подобны с коэффициентом 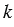 = 1. Справедливо и обратное утверждение:
= 1. Справедливо и обратное утверждение:
|
Если два многоугольника подобны и коэффициент подобия равен единице, то такие многоугольники равны.
|
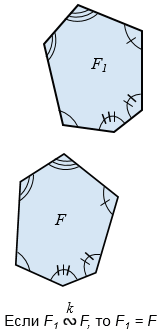
Рис. 2
Обратите внимание, нам известно, что два треугольника подобны, если углы одного треугольника соответственно равны углам другого, или если стороны одного треугольника пропорциональны сторонам другого. Для произвольных многоугольников аналогичные свойства не верны. Например, прямоугольник и квадрат, изображённые на рисунке 3, 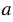 , не подобны, хотя углы их соответственно равны; квадрат и ромб, изображённые на рисунке 3, б, также не являются подобными, хотя и имеют пропорциональные стороны.
, не подобны, хотя углы их соответственно равны; квадрат и ромб, изображённые на рисунке 3, б, также не являются подобными, хотя и имеют пропорциональные стороны.
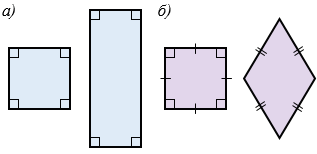
Рис. 3
Советуем посмотреть:
Теоремы о периметрах и площадях подобных фигур
Применение подобия фигур к доказательству теорем и решению задач
Правило встречается в следующих упражнениях:
7 класс
Задание 1298, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1299, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1302, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1303, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1304, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1306, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1308, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1320, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1335, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 3, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник