Наложения и движения

Мы знаем, что фигура Ф равна фигуре Ф₁, если фигуру Ф можно совместить наложением с фигурой Ф₁. Под наложением фигуры Ф на фигуру Ф₁ мы понимаем некоторое отображение фигуры Ф на фигуру Ф₁. При этом любая точка плоскости отображается в определенную точку плоскости, значит, наложение - это отображение плоскости на себя. Наложения - это такие отображения плоскости на себя, которые обладают свойствами, выраженными в аксиомах (аксиомы о наложении и равенстве фигур).

Утверждение:

При наложении различные точки отображаются в различные точки.

Доказательство:

Предположим, что при некотором наложении какие-то две точки А и В отображаются в одну и ту же точку С. Тогда фигура Ф₁, которая состоит из точек А и В, равна фигуре Ф₂, состоящей из одной точки С. Отсюда следует, что Ф₂=Ф₁ (т.к. согласно аксиоме, если фигура Ф равна фигуре Ф₁, то фигура Ф₁ равна фигуре Ф), т.е. при некотором наложении фигура Ф₂ отображается в фигуру Ф₁. Но это не возможно так как наложение - это отображение, а при любом отображении точке С ставится только одна точка плоскости. Значит, наше предположение неверно и две точки А и В не могут отображаться в одну и ту же точку.

Из этого утверждения мы можем сделать вывод, что при наложении отрезок отображается на равный ему отрезок. Пусть при наложении концы А и В отрезка АВ отображаются в точки А₁ и В₁. Тогда отрезок АВ отображается на отрезок А₁В₁ (т.к. согласно аксиоме, если при наложении совмещаются концы двух отрезков, то совмещаются и сами отрезки), и, следовательно, АВ=А₁В₁. Так как равные отрезки имеют равные длины, то наложение является отображением плоскости на себя, которое сохраняет расстояния, то есть любое наложение является движением плоскости.

Теорема

Доказательство

Дано: движение 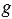, АВС отображается в А₁В₁С₁, АВС=А₁В₁С₁

Доказать: движение 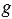- наложение

Доказательство:

Так как АВС=А₁В₁С₁ , то по определению существует наложение 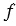, при котором точки А, В и С отображаются в точки А₁, В₁ и С₁ соответственно. Докажем, что 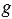совпадает с .

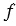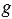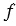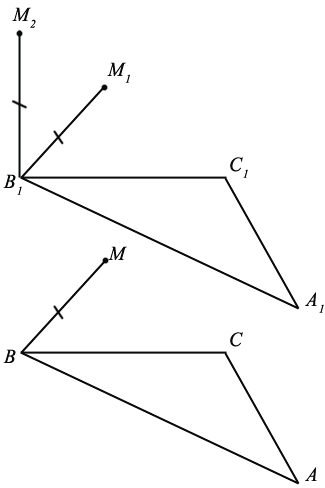
Предположим обратное. Тогда найдется хотя бы одна точка М, которая при движении отображается в точку М₁, а при наложении отображается в другую точку М₂. При отображениях 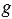и 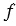сохраняются расстояния, поэтому ВМ=В₁М₁, ВМ=В₁М₂, отсюда В₁М₁=В₂М₂, то есть точка В₁ равноудалена от точек М₁ и М₂.

Аналогично можно  доказать, что точки А₁ и С₁ равноудалены от точек М₁ и М₂. Следовательно, точки А₁, В₁, и С₁ лежат на серединном перпендикуляре к отрезку М₁М₂, но это не возможно, так как вершины А₁В₁С₁ не лежат на одной прямой. Значит, наше предположение неверно и отображение 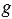совпадает с 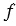, другими словами, движение 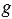является наложением. Теорема доказана.

Следствие