Разложение вектора по двум неколлинеарным векторам
Лемма
Если векторы  и и  коллинеарны и коллинеарны и 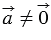 , то существует такое число , то существует такое число 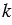 , что , что  . . |
Доказательство
Дано:  и
и  коллинеарны,
коллинеарны, 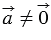 .
.
Доказать: существует такое число 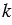 , что
, что  .
.
Доказательство:
Возможны два случая:
1) 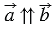 .
.
Пусть число 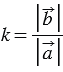 . Так как
. Так как 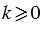 , то векторы
, то векторы 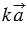 и
и  сонаправлены.
сонаправлены.
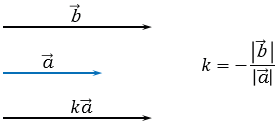
При этом, их длины равны: 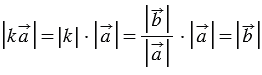 . Следовательно,
. Следовательно,  .
.
2) 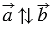 .
.
Пусть число 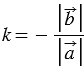 . Так как
. Так как 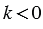 , то векторы
, то векторы 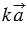 и
и  сонаправлены.
сонаправлены.
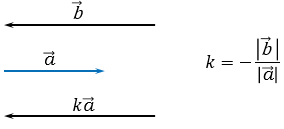
При этом, их длины равны: 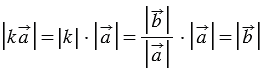 . Следовательно,
. Следовательно,  . Лемма доказана.
. Лемма доказана.
Пусть  и
и  два данных вектора. Если вектор
два данных вектора. Если вектор 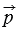 представлен в виде
представлен в виде 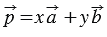 , где
, где 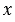 и
и 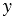 - некоторые числа, то говорят, что вектор
- некоторые числа, то говорят, что вектор 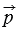 разложен по векторам
разложен по векторам  и
и  . Числа
. Числа 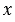 и
и 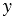 называются коэффициентами разложения.
называются коэффициентами разложения.
Теорема
| На плоскости любой вектор можно разложить по двум данным неколлинеарным векторам, причем коэффициенты разложения определяются единственным образом. |
Доказательство
Дано:  и
и  неколлинеарные.
неколлинеарные.
Доказать: любой вектор 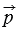 можно разложить по векторам
можно разложить по векторам  и
и  , т.е.
, т.е. 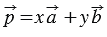 ,
, 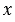 и
и 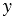 определяются единственным образом.
определяются единственным образом.
Доказательство:
1 случай
Вектор  коллинеарен одному из векторов
коллинеарен одному из векторов  и
и  , например, вектору
, например, вектору  .
.
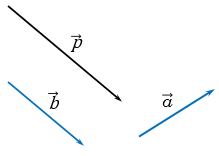
Тогда по лемме о коллинеарных векторах вектор 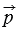 можно представить в виде
можно представить в виде 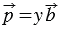 , где
, где 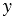 - некоторое число, следовательно,
- некоторое число, следовательно, 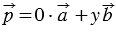 , т.е. вектор
, т.е. вектор 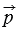 можно разложить по векторам
можно разложить по векторам  и
и  .
.
2 случай
Вектор 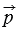 не коллинеарен ни вектору
не коллинеарен ни вектору  , ни вектору
, ни вектору  .
.
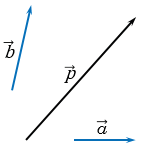
Отметим какую-нибудь точку О и отложим от нее векторы 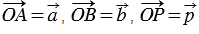 . Через точку Р проведем прямую, параллельную прямой ОВ, которая пересечет прямую ОА в точке А1.
. Через точку Р проведем прямую, параллельную прямой ОВ, которая пересечет прямую ОА в точке А1.
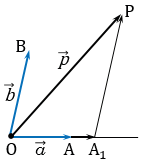
По правилу треугольника сложения двух векторов 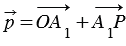 , при этом векторы
, при этом векторы 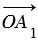 и
и 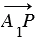 коллинеарны векторам
коллинеарны векторам  и
и  , следовательно, по лемме о коллинеарных векторах существуют такие числа
, следовательно, по лемме о коллинеарных векторах существуют такие числа 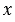 и
и 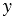 такие, что
такие, что 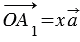 и
и 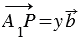 . Поэтому
. Поэтому 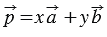 , т.е. вектор
, т.е. вектор 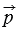 можно разложить по векторам
можно разложить по векторам  и
и  .
.
Докажем, что коэффициенты 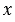 и
и 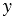 определяются единственным образом.
определяются единственным образом.
Допустим, что вместе с разложением 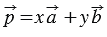 (1) существует и другое разложение
(1) существует и другое разложение 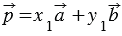 . (2)
. (2)
Вычтем из равенства (1) равенство (2), получим: 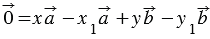 , откуда, учитывая правила действий над векторами,
, откуда, учитывая правила действий над векторами, 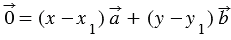 . (3)
. (3)
Равенство (3) выполнимо только в том случае, когда 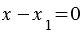 и
и 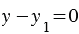 . Действительно, если предположить, что
. Действительно, если предположить, что 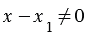 , то из равенства (3) получим, что
, то из равенства (3) получим, что 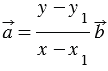 , значит, векторы
, значит, векторы  и
и  коллинеарны, что противоречит условию теоремы. Следовательно,
коллинеарны, что противоречит условию теоремы. Следовательно, 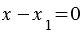 и
и 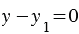 , откуда
, откуда 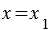 и
и 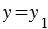 , а это говорит о том, что коэффициенты
, а это говорит о том, что коэффициенты 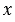 и
и 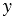 разложения вектора
разложения вектора 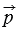 определяются единственным образом. Теорема доказана.
определяются единственным образом. Теорема доказана.
Советуем посмотреть:
Связь между координатами вектора его начала и конца
Простейшие задачи в координатах
Взаимное расположение двух окружностей
Правило встречается в следующих упражнениях:
7 класс
Задание 911, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 914, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 916, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 918, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 919, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 920, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 921, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 927, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 988, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник