Уравнение линии на плоскости

В курсе алгебры строятся графики некоторых функций, например график функции 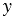= 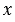. Известно, что графиком этой функции является прямая, которая проходит через точки О (0;0) и А (1; 1):

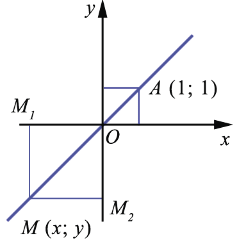
Координаты любой точки М ( 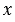; 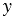), которая лежит на прямой ОА, удовлетворяют уравнению 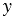= 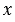(так как ММ₁ = ММ₂), а координаты любой точки, которая не лежит на прямой ОА, этому уравнению не удовлетворяют. Говорят, что уравнение 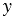= 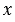является уравнением прямой ОА. Введём теперь понятие уравнения произвольной линии.

Пусть на плоскости задана прямоугольная система координат 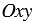и дана некоторая линия :

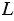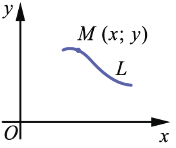
Уравнением линии 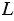, заданной на данной плоскости, называют уравнение с двумя переменными 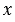и , и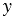меющие такие свойства:

1) если точка принадлежит линии 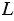, то её координаты являются решением данного уравнения;

2) любое решение (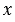; 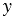) данного уравнения является координатами точки, принадлежащей линии .

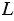При изучении линий методом координат возникают две задачи:

1. по геометрическим свойствам данной линии найти её уравнение;

2. обратная задача: по заданному уравнению линии исследовать её геометрические свойства (рассматривается в курсе алгебры).