Взаимное расположение двух окружностей
Исследуем взаимное расположение двух окружностей в зависимости от их радиусов 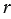 ,
,  и расстояния между их центрами
и расстояния между их центрами 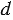 . Пусть
. Пусть 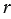
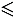
 .
.
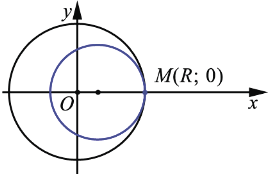
Если центры окружностей совпадают, т.е. 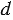 = 0, то окружности называются концентрическими, и окружность радиуса
= 0, то окружности называются концентрическими, и окружность радиуса 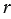 лежит внутри круга радиуса
лежит внутри круга радиуса  :
:
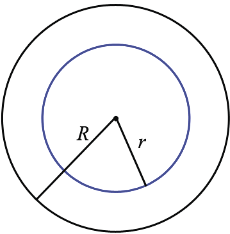
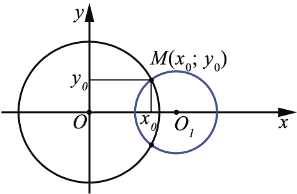
Пусть 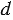
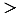 0. Введём прямоугольную систему координат
0. Введём прямоугольную систему координат 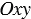 так, чтобы точка
так, чтобы точка 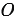 совпала с центром окружности радиуса
совпала с центром окружности радиуса  , а точка
, а точка 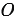 1 с координатами
1 с координатами 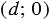 являлась центром второй окружности. Тогда в данной системе координат уравнения первой и второй окружностей имеют вид:
являлась центром второй окружности. Тогда в данной системе координат уравнения первой и второй окружностей имеют вид:
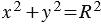 ,
, 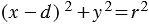 . (1)
. (1)
Если система уравнений (1) имеет решением пару чисел 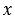 =
= 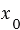 ,
, 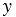 =
= 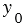 , то точка
, то точка 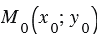 - общая точка данных окружностей, и обратно: если точка
- общая точка данных окружностей, и обратно: если точка 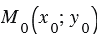 - общая точка данных окружностей, то пара чисел
- общая точка данных окружностей, то пара чисел 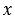 =
= 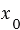 ,
, 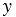 =
=  является решением системы уравнений (1):
является решением системы уравнений (1):
Пусть система (1) имеет решением пару чисел  =
=  ,
, 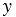 =
= 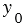 , т.е. справедливы числовые равенства
, т.е. справедливы числовые равенства
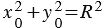 ,
, 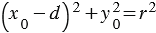 . (2)
. (2)
Вычтем второе равенство из первого, получим равенство 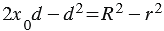 . Выражаем из данного равенства
. Выражаем из данного равенства 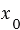 :
:
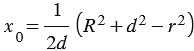 . (3)
. (3)
Так как 
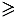
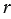 и
и 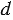
 0, то
0, то 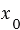
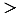 0. В то же время из первого равенства (2) следует, что
0. В то же время из первого равенства (2) следует, что 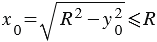 , т.е. для величин
, т.е. для величин  ,
, 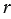 и
и 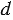 должно выполняться неравенство
должно выполняться неравенство 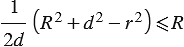 или
или 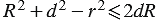 . Последнее неравенство запишем в виде
. Последнее неравенство запишем в виде 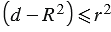 . Следовательно,
. Следовательно, 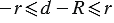 или
или
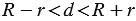 . (4)
. (4)
Отметим, что 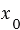 =
=  , если
, если 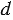 =
=  -
- 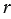 или
или 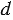 =
=  +
+ 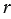 , и
, и 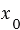
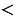
 , если
, если 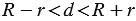 .
.
Итак, если система уравнений (1) имеет решение, то величина 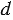 удовлетворяет неравенствам (4). Поэтому, если не выполнено какое-то из неравенств (4), то система (1) не имеет решений и данные окружности не имеют общих точек. Так может быть в двух случаях:
удовлетворяет неравенствам (4). Поэтому, если не выполнено какое-то из неравенств (4), то система (1) не имеет решений и данные окружности не имеют общих точек. Так может быть в двух случаях:
1. 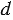
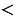
 -
- 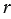 , т.е.
, т.е. 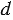 +
+ 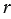
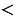
 :
:
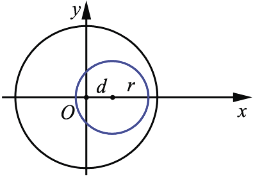
В этом случае окружность радиуса 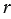 лежит внутри круга радиуса
лежит внутри круга радиуса  . Говорят также, что одна окружность лежит внутри другой.
. Говорят также, что одна окружность лежит внутри другой.
2. 
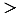
 +
+ 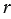 :
:
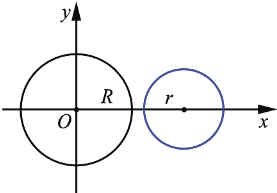
В этом случае говорят, что одна окружность лежит вне другой.
Если неравенства (4) выполнены, то возможны три случая:
3. 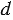 =
=  -
- 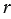 , при этом из того что
, при этом из того что 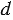
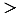 0 следует, что
0 следует, что 
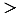
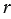 . Выше мы говорили, что
. Выше мы говорили, что 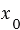 =
= , поэтому из первого из равенств (2) следует, что
, поэтому из первого из равенств (2) следует, что 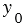 =0. Подставив пару чисел
=0. Подставив пару чисел 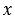 =
=  ,
, 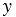 =0 в систему равенств (4), мы получим, что данные числа являются ее решением. Значит, в данном случае окружности имеют ровно одну общую точку:
=0 в систему равенств (4), мы получим, что данные числа являются ее решением. Значит, в данном случае окружности имеют ровно одну общую точку:
Говорят, что окружности касаются изнутри.
4.  =
=  +
+  . В данном случае также
. В данном случае также  =
= , поэтому
, поэтому  =0. Подставив пару чисел
=0. Подставив пару чисел  =
=  ,
,  =0 в систему равенств (4), мы получим, что данные числа являются ее решением. В данном случае, как и в случае 3, окружности имеют одну общую точку, но расположены друг относительно друга иначе:
=0 в систему равенств (4), мы получим, что данные числа являются ее решением. В данном случае, как и в случае 3, окружности имеют одну общую точку, но расположены друг относительно друга иначе:
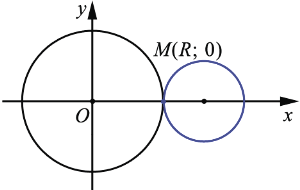
Говорят, что окружности касаются извне.
5. 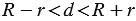 . Выше мы говорили, что число
. Выше мы говорили, что число 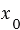 , которое определяется равенством (3), удовлетворяет неравенству
, которое определяется равенством (3), удовлетворяет неравенству 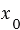
 , поэтому из первого равенства (2) получаем два значения
, поэтому из первого равенства (2) получаем два значения 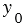 :
: 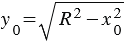 и
и 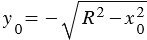 . То есть в данном случае система (1) имеет два решения:
. То есть в данном случае система (1) имеет два решения: 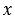 =
= 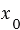 ,
, 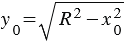 и
и 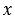 =
= 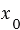 ,
, 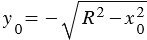 :
:
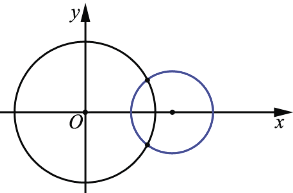
Следовательно, окружности пересекаются в двух точках.
Итак, если расстояние между центрами двух окружностей отлично от нуля, то возможны пять случаев, описанных выше, взаимного расположения двух окружностей.
Советуем посмотреть:
Разложение вектора по двум неколлинеарным векторам
Связь между координатами вектора его начала и конца
Простейшие задачи в координатах
Правило встречается в следующих упражнениях:
7 класс
Задание 1290, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник