Уравнение прямой

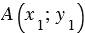Выведем уравнение данной прямой в заданной прямоугольной системе координат. Отметим две точки и 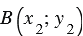так, чтобы прямая была серединным перпендикуляром к отрезку :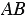

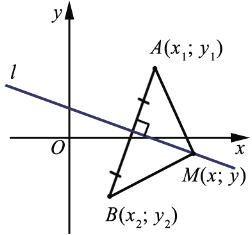
Возьмем точку 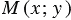, лежащую на прямой , тогда 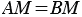или 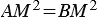, значит, координаты точки 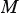удовлетворяют уравнению

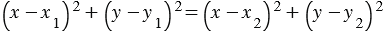.    (1)

В тоже время, если взять точку 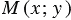, не лежащую на прямой , то ее координаты не будут удовлетворять уравнению (1). Следовательно, уравнение (1) является уравнением прямой  в заданной системе координат. Возведем выражения в скобках в квадрат:

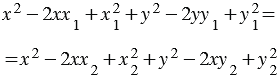
Приведем подобные члены:

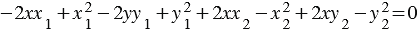
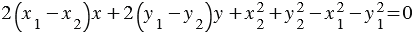
Тогда уравнение  (1) примет вид 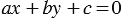, (2) где 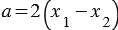, , 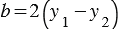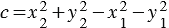. Из того что  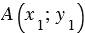и 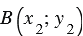- различные точки, следует что хотя бы одна из разносте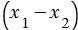й и 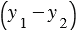не равна нулю, т.е. хотя бы один из коэффициентов 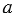и 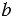отличен от нуля.

Уравнение прямой в прямоугольной системе координат является уравнением первой степени.

Если в уравнении (2) 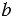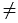0, то его можно записать так:

,

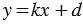где 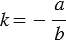, 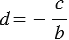. Число 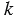называется угловым коэффициентом прямой, заданной этим уравнением.

• две параллельные прямые, не параллельные оси 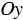, имеют одинаковые угловые коэффициенты;
• если две прямые имеют одинаковые угловые коэффициенты, то эти прямые параллельны.

Докажем данные утверждения.

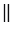
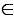
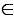
Дано: _{1 2}, М₁, С_{1 1}, М₂, С_{2 1}

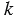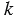Доказать: ₁ = ₂

Доказательство:

Выберем точки М₁ и М₂ на данных прямых так, чтобы их ординаты были равны, т.е. прямая М₁М₂ параллельна оси 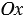, а точки С₁, С₂ :

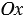Рассмотрим С₁М₁М₂С₂: по условию _{1 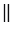2}, а по построению М₁М₂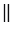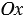, значит, по определению рассматриваемый четырехугольник параллелограмм. По свойству параллелограмма имеем: М₁М₂ = С₁С₂, С₁М₁ = С₂М₂.

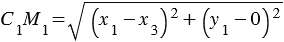
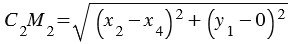
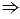
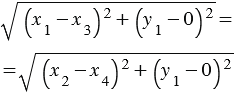
Возведем левую и правую части в квадрат:

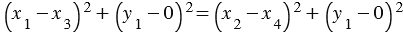
или

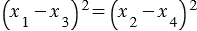, откуда имеем, что .

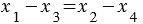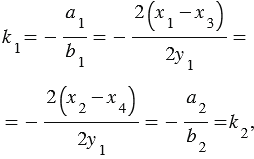
что и требовалось доказать.

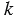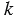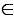
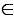
Дано: ₁ = ₂, М₁, С_{1 1}, М₂, С_{2 1}

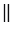
Доказать: _{1 2}

Доказательство:

Выберем точки М₁ и М₂ на данных прямых так, чтобы их ординаты были равны, т.е. прямая М₁М₂ параллельна оси 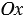, а точки С₁, С₂ :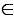

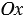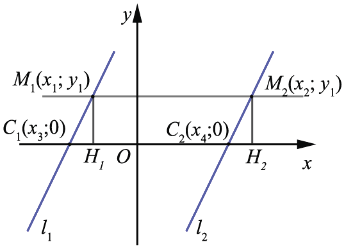
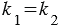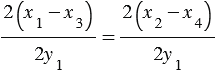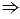
, т.е. ,   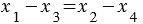или .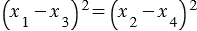

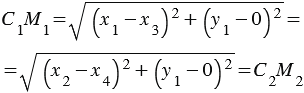
Опустим высоты М₁Н₁ и М₂Н₂ и рассмотрим 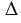С₁М₁Н₁ и 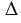С₂М₂Н₂: М₁Н₁ = М₂Н₂, как расстояние между параллельными прямыми, С₁М₁ = С₂М₂(по доказанному выше),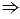 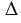С₁М₁Н₁ и 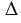С₂М₂Н₂ (по гипотенузе и катету), а в равных треугольниках напротив соответственно равных сторон лежат равные углы, поэтому 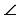М₁С₁Н₁ = 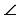М₂С₂Н₂, но если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны, значит, _{1 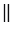2}, что и требовалось доказать.

Выведем уравнение прямой , проходящей через точку 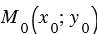и параллельной оси :

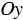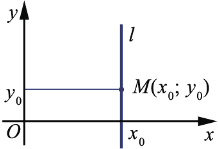
Абсцисса любой точки 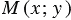, которая лежит на прямой , равна 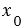, иными словами, координаты любой точки 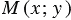прямой удовлетворяют уравнению 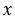= 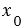. В  тоже время координаты любой точки, которая не лежит на данной прямой, этому уравнению не удовлетворяют. Значит, уравнение 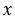= 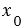является уравнением прямой .

Очевидно, что ось 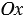имеет уравнение 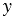= 0, а ось 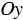- уравнение 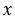= 0.