Задание 638 - ГДЗ Геометрия 7-9 класс. Атанасян. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№638 учебника 2013-2022 (стр. 166):
Прямая АВ касается окружности с центром О радиуса 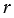 в точке В. Найдите АВ, если ОА = 2 см, а
в точке В. Найдите АВ, если ОА = 2 см, а 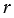 = 1,5 см.
= 1,5 см.
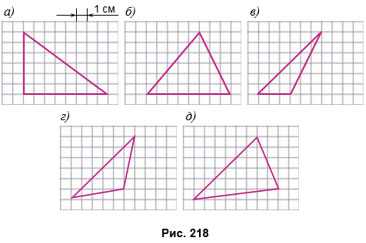
№638 учебника 2023-2024 (стр. 161):
Подсказка
№638 учебника 2013-2022 (стр. 166):
Вспомните:
- Что такое окружность, ее элементы.
- Что называется касательной к окружности, ее свойства.
- Какой треугольник называется прямоугольным.
- Теорему Пифагора.
№638 учебника 2023-2024 (стр. 161):
Вспомните:
- Как найти площадь треугольника.
- Какой треугольник называется прямоугольным.
- Как найти площадь квадрата.
- Как найти площадь прямоугольника.
- Свойства площадей.
Ответ
№638 учебника 2013-2022 (стр. 166):
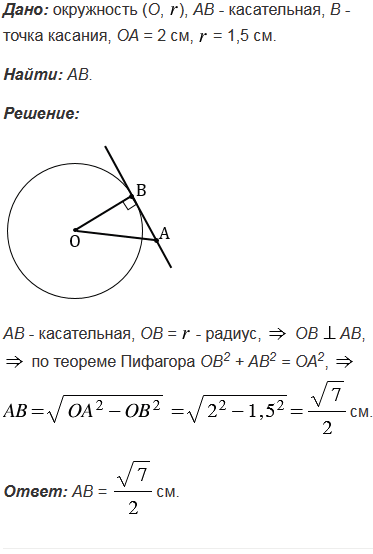

№638 учебника 2023-2024 (стр. 161):
а) 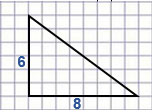
S =  • 8 • 6 =
• 8 • 6 =  • 48 = 24 (см2).
• 48 = 24 (см2).
Ответ: 24 см2.
б) 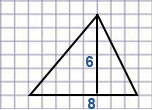
S =  • 8 • 6 =
• 8 • 6 =  • 48 = 24 (см2).
• 48 = 24 (см2).
Ответ: 24 см2.
в) Sкв. = S + S1 + S2
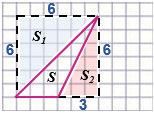
S = Sкв. - (S1 + S2)
Sкв. = 62 = 36 (см2).
S1 =  • 6 • 6 =
• 6 • 6 =  • 36 = 18 (см2).
• 36 = 18 (см2).
S2 =  • 6 • 3 =
• 6 • 3 =  • 18 = 9 (см2).
• 18 = 9 (см2).
S = Sкв. - (S1 + S2) = 36 - (18 + 9) =
= 36 - 27 = 9 (см2).
Ответ: 9 см2.
г) Sкв. = S + S1 + 2S2 + S3
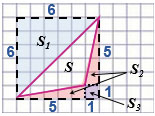
S = Sкв. - (S1 + 2S2 + S3).
Sкв. = 62 = 36 (см2).
S1 =  • 6 • 6 =
• 6 • 6 =  • 36 = 18 (см2).
• 36 = 18 (см2).
S2 =  • 5 • 1 =
• 5 • 1 =  • 5 = 2,5 (см2).
• 5 = 2,5 (см2).
S3 = 12 = 1 (см2).
S = Sкв. - (S1 + 2S2 + S3) =
= 36 - (18 + 2 • 2,5 + 1) =
= 36 - 24 = 12 (см2).
Ответ: 12 см2.
д) Sпр. = S + S1 + S2 + S3
S = Sпр. - (S1 + S2 + S3).
Sпр. = 8 • 6 = 48 (см2).
S1 =  • 6 • 6 =
• 6 • 6 =  • 36 = 18 (см2).
• 36 = 18 (см2).
S2 =  • 5 • 2 =
• 5 • 2 =  • 10 = 5 (см2).
• 10 = 5 (см2).
S3 =  • 8 • 1 =
• 8 • 1 =  • 8 = 4 (см2).
• 8 = 4 (см2).
S = Sпр. - (S1 + S2 + S3) =
= 48 - (18 + 5 + 4) = 48 - 27 = 21 (см2).
Ответ: 21 см2.
Пояснения:
а) Площадь прямоугольного треугольника равна половине произведения его катетов.

S =  • 6 • 8 =
• 6 • 8 =  • 48 = 24 (см2).
• 48 = 24 (см2).
б) Площадь треугольника равна половине произведения его основания на высоту, проведенную к этому основанию.

S =  • 8 • 6 =
• 8 • 6 =  • 48 = 24 (см2).
• 48 = 24 (см2).
в) Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников.
Дочертим данный нам треугольник до квадрата со стороной, равной 6 см.

Квадрат составлен из треугольника с площадью S и двух прямоугольных треугольников с площадями S1 и S2, тогда
Sкв. = S + S1 + S2, откуда
S = Sкв. - (S1 + S2)
Площадь квадрата равна квадрату его стороны.
Sкв. = 62 = 36 (см2).
Площадь прямоугольного треугольника равна половине произведения его катетов.
S1 =  • 6 • 6 =
• 6 • 6 =  • 36 = 18 (см2).
• 36 = 18 (см2).
S2 =  • 6 • 3 =
• 6 • 3 =  • 18 = 9 (см2).
• 18 = 9 (см2).
Получаем:
S = Sкв. - (S1 + S2) = 36 - (18 + 9) =
= 36 - 27 = 9 (см2).
г) Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников.
Дочертим данный нам треугольник до квадрата со стороной, равной 6 см.

Квадрат составлен из треугольника с площадью S, трех прямоугольных треугольников с площадями S1, S2, S2 и квадратика с площадью S3, тогда
Sкв. = S + S1 + 2S2 + S3, откуда
S = Sкв. - (S1 + 2S2 + S3).
Площадь квадрата равна квадрату его стороны.
Sкв. = 62 = 36 (см2).
Площадь прямоугольного треугольника равна половине произведения его катетов.
S1 =  • 6 • 6 =
• 6 • 6 =  • 36 = 18 (см2).
• 36 = 18 (см2).
S2 =  • 5 • 1 =
• 5 • 1 =  • 5 = 2,5 (см2).
• 5 = 2,5 (см2).
Площадь квадрата равна квадрату его стороны.
S3 = 12 = 1 (см2).
Получаем:
S = Sкв. - (S1 + 2S2 + S3) =
= 36 - (18 + 2 • 2,5 + 1) =
= 36 - 24 = 12 (см2).
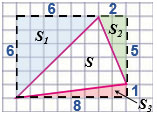
д) Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников.
Дочертим данный нам треугольник до прямоугольника со сторонами, равными 6 см и 8 см.

Прямоугольник составлен из треугольника с площадью S и трех прямоугольных треугольников с площадями S1, S2, S3, тогда
Sпр. = S + S1 + S2 + S3, откуда
S = Sпр. - (S1 + S2 + S3).
Площадь прямоугольника равна произведению его смежных сторон (длины и ширины).
Sпр. = 8 • 6 = 48 (см2).
Площадь прямоугольного треугольника равна половине произведения его катетов.
S1 =  • 6 • 6 =
• 6 • 6 =  • 36 = 18 (см2).
• 36 = 18 (см2).
S2 =  • 5 • 2 =
• 5 • 2 =  • 10 = 5 (см2).
• 10 = 5 (см2).
S3 =  • 8 • 1 =
• 8 • 1 =  • 8 = 4 (см2).
• 8 = 4 (см2).
Получаем:
S = Sпр. - (S1 + S2 + S3) =
= 48 - (18 + 5 + 4) = 48 - 28 = 21 (см2).
Вернуться к содержанию учебника