Задание 484 - ГДЗ Геометрия 7-9 класс. Атанасян. Учебник
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
Выберите год учебника
№484 учебника 2013-2022 (стр. 132):
В прямоугольном треугольнике 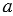 и
и 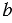 - катеты, - гипотенуза. Найдите
- катеты, - гипотенуза. Найдите 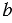 , если:
, если:
а) 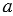 = 12,
= 12, 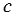 = 13;
= 13;
б) 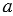 = 7,
= 7, 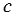 = 9;
= 9;
в) 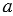 = 12,
= 12, 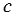 = 2
= 2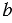 ;
;
г) 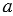 =
= 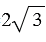 ,
, 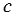 = 2
= 2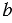 ;
;
д) 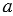 = 3
= 3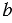 ,
, 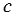 =
= 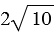 .
.
№484 учебника 2023-2024 (стр. 128):
Подсказка
№484 учебника 2013-2022 (стр. 132):
Вспомните:
- Какой треугольник называется прямоугольным, его элементы.
- Теорему Пифагора.
№484 учебника 2023-2024 (стр. 128):
Вспомните:
- Что называют треугольником.
- Какая точка является серединой отрезка.
- Какие прямые называют параллельными.
- Признаки параллельности двух прямых.
- Первый признак равенства треугольников.
- Свойства равных треугольников.
- Какой четырехугольник называют параллелограммом.
- Признаки параллелограмма.
- Какие углы называют вертикальными.
Ответ
№484 учебника 2013-2022 (стр. 132):

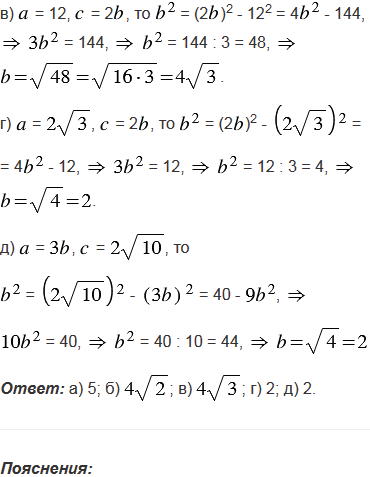

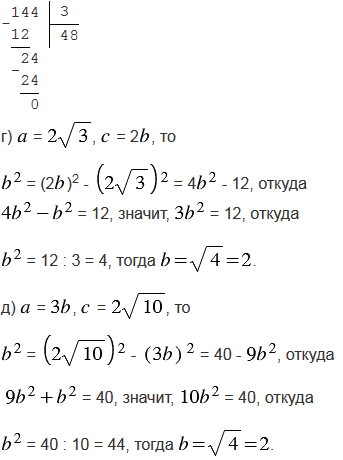
№484 учебника 2023-2024 (стр. 128):
Дано: 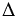 АВС, MN - средняя линия.
АВС, MN - средняя линия.
Доказать: MN 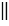 АВ и MN =
АВ и MN = 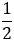 АВ.
АВ.
Доказательство:
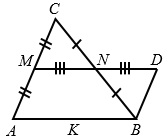
1. Отложим на прямой МN отрезок ND = MN.
2. В 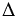 СМN и
СМN и 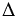 BND:
BND:
ND = MN, СN = BN (т.к. N - середина ВС),  СNM =
СNM =  BND (вертикальные углы),
BND (вертикальные углы), 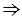
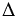 СМN =
СМN = 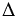 BND по 1 признаку равенства треугольников,
BND по 1 признаку равенства треугольников, 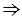 ВD = СМ и
ВD = СМ и  NBD =
NBD =  СNМ,
СNМ, 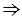 ВD = АМ (т.к. М - середина АС и СМ = АМ) и АС
ВD = АМ (т.к. М - середина АС и СМ = АМ) и АС 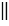 ВD (1 признак параллельности),
ВD (1 признак параллельности), 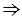 АМDВ - параллелограмм (по признаку параллелограмма),
АМDВ - параллелограмм (по признаку параллелограмма), 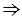 МD
МD 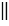 АВ и МD = AB,
АВ и МD = AB, 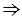 MN
MN 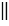 АВ и MN =
АВ и MN = 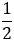 АВ (т.к. по построению ND = MN). Что и требовалось доказать.
АВ (т.к. по построению ND = MN). Что и требовалось доказать.
Пояснения:
Чтобы выполнить доказательство делаем дополнительное построение: отложим на прямой МN отрезок ND, равный отрезку МN, т.е. ND = MN.
Теперь рассмотрим треугольники СМN и BND:
1. ND = MN по построению;
2. СN = BN, т.к. по условию MN - средняя линия 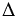 АВС, значит, N - середина ВС;
АВС, значит, N - середина ВС;
3.  СNM =
СNM =  BND, так как эти углы вертикальные.
BND, так как эти углы вертикальные.
Следовательно, 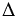 СМN =
СМN = 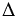 BND по 1 признаку равенства треугольников (по двум сторонам и углу между ними).
BND по 1 признаку равенства треугольников (по двум сторонам и углу между ними).
В равных треугольниках против равных сторон лежат равные углы и, наоборот. Значит, ВD = СМ и  NBD =
NBD =  СNМ.
СNМ.
ВD = СМ и СМ = АМ, т.к. по условию MN - средняя линия 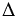 АВС, значит, М - середина АС, следовательно, ВD = АМ.
АВС, значит, М - середина АС, следовательно, ВD = АМ.
 NBD =
NBD =  СNМ и эти углы накрест лежащие при пересечении прямых АС и ВD секущей ВС, значит, АС
СNМ и эти углы накрест лежащие при пересечении прямых АС и ВD секущей ВС, значит, АС 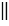 ВD по 1 признаку параллельности двух прямых.
ВD по 1 признаку параллельности двух прямых.
Итак, ВD = АМ и АМ 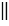 ВD (АМ лежит на АС), следовательно, четырехугольник АМDВ - параллелограмм по признаку параллелограмма. В параллелограмме противоположные стороны параллельны и равны, значит, МD
ВD (АМ лежит на АС), следовательно, четырехугольник АМDВ - параллелограмм по признаку параллелограмма. В параллелограмме противоположные стороны параллельны и равны, значит, МD 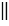 АВ и МD = AB. При этом по построению ND = MN, тогда MN =
АВ и МD = AB. При этом по построению ND = MN, тогда MN = 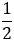 МD, следовательно, MN =
МD, следовательно, MN = 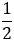 АВ. Что и требовалось доказать.
АВ. Что и требовалось доказать.
Вернуться к содержанию учебника