Задание 4.72 - ГДЗ Математика 5 класс. Виленкин, Жохов. Учебник часть 1. Страница 140
Старая и новая редакции
Вернуться к содержанию учебника
Вопрос
№4.72 учебника 2023-2024 (стр. 140):
№4.72 учебника 2021-2022 (стр. 140):
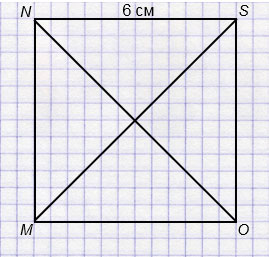
В квадрате MNSO со стороной 6 см проведены отрезки МS и NO.
а) Найдите площадь каждого из четырех получившихся треугольников.
б) Из двух треугольников сложили новый квадрат. Найдите его площадь.
Подсказка
№4.72 учебника 2023-2024 (стр. 140):
№4.72 учебника 2021-2022 (стр. 140):
Вспомните:
- Что называют квадратом, его площадь.
- Что называют треугольником.
- Какие фигуры называют равными.
- Свойства площадей.
- Деление чисел.
- Степень с натуральным показателем.
- Умножение чисел.
Ответ
№4.72 учебника 2023-2024 (стр. 140):
№4.72 учебника 2021-2022 (стр. 140):
а) 62 = 36 (см2) - площадь квадрата.
36 : 4 = 9 (см2) - площадь каждого из четырех треугольников.
б) 9 • 2 = 18 (см2)
Ответ: площадь одного треугольника 9 см2; площадь квадрата из двух треугольников равна 18 см2.
Пояснения:
Площадь квадрата равна квадрату его стороны. Тогда площадь квадрата со стороной 6 см равна:
62 = 6 • 6 = 36 (см2).
Отрезки МS и NO делят квадрат MNSO на четыре равных треугольника, площади которых равны друг другу и равны площади квадрата, деленной на 4, то есть:
36 : 4 = 9 (см2).
Если квадрат составить из двух треугольников, то площадь квадрата будет равна сумме площадей этих треугольников (свойство площадей). При этом, учитывая то, что площади треугольников равны, сложение можно заменить умножением. Тогда площадь квадрата, составленного из двух треугольников, площадь каждого из которых 9 см2, будет равна:
9 • 2 = 18 (см2).
Вернуться к содержанию учебника