Упражнение 740 - ГДЗ Алгебра 9 класс. Макарычев, Миндюк. Учебник. Страница 196

Пусть скорость лодки в стоячей воде равна \(x\) км/ч (\(x >0\)).

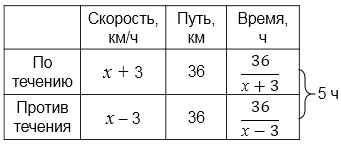
Составим уравнение:

\(\frac{36}{x+3}+\frac{36}{x-3}=5\) \(/\times (x-3)(x+3)\)

\(36(x-3) + 36(x+3) = 5(x-3)(x+3)\)

\(36x - 108 + 36x + 108 = 5(x^2 - 9)\)

\(72x = 5x^2 - 45\)

\(5x^2 - 72x - 45 = 0\)

\(a = 5\),  \(b = -72\),  \(c = -45\)

\(D = b^2 - 4ac =\)

\[=(-72)^2-4\cdot 5\cdot (-45)=\]

\(=5184+900=6084 > 0\) - два действительных корня.

\(x_{1,2} = \frac{-b \pm \sqrt D}{2a}\),   \(\sqrt{6084}=78\)

\[x_1=\frac{72 + 78}{2\cdot5}=\frac{150}{10}=15\]

\(x_2=\frac{72 - 78}{2\cdot5}=\frac{-6}{10}=-0,6\) - не удовлетворяет условию.

\[v_1=\frac{150}{10}=15\]

\[v_2=\frac{-6}{10}=-0{,}6\]

Ответ: скорость лодки в стоячей воде равна \(15\) км/ч.

Пояснения:

Скорость лодки по течению равна сумме собственной скорости лодки и скорости течения реки, скорость лодки против течения равна разности собственной скорости лодки и скорости течения реки.

Время в пути вычисляется по формуле:

\[t=\frac{s}{v},\]

где \(s\) - пройденный путь,

\(v\) - скорость движения.

Обозначим скорость лодки в стоячей воде через \(x\). Тогда скорость по течению равна \(x+3\), а против течения — \(x-3\).

Время движения по течению:

\[\frac{36}{x+3}\]

Время движения против течения:

\[\frac{36}{x-3}\]

Суммарное время равно \(5\) часов:

\[\frac{36}{x+3}+\frac{36}{x-3}=5.\]

Домножив обе части уравнения на общий знаменатель дробей и выполнив преобразования, получаем квадратное уравнение:

\(5x^2-72x-45=0\).

Полное квадратное уравнение

\[ax^2+bx+c=0\]

решаем через дискриминант

\[D=b^2-4ac.\]

Если \(D > 0\), то уравнение имеет два действительных корня:

\[x_{1,2}=\frac{-b\pm \sqrt{D}}{2a}.\]

Отрицательный корень не подходит, так как скорость не может быть отрицательным числом, поэтому берём положительный корень \(x=15\) км/ч.